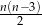Zadanie nr 2464063
Oblicz liczbę przekątnych wielokąta wypukłego o  bokach.
bokach.
Rozwiązanie
Możemy zacząć od rysunku.
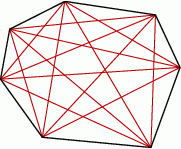
Sposób I
Z każdego wierzchołka wychodzi 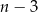 przekątnych (odejmujemy 3 wierzchołki: ten, na który patrzymy i dwa sąsiednie). W sumie mamy więc
przekątnych (odejmujemy 3 wierzchołki: ten, na który patrzymy i dwa sąsiednie). W sumie mamy więc 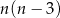 przekątnych. To jednak jest źle, bo każdą przekątną policzyliśmy dwukrotnie (w obu końcach). Zatem liczba przekątnych wynosi
przekątnych. To jednak jest źle, bo każdą przekątną policzyliśmy dwukrotnie (w obu końcach). Zatem liczba przekątnych wynosi 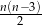 .
.
Sposób II
Wszystkich par wierzchołków jest
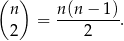
Tyle samo jest odcinków między dwoma wierzchołkami  –kąta. Nie każdy odcinek jest jednak przekątną. Jakie nie są? – dokładnie boki. Boków mamy
–kąta. Nie każdy odcinek jest jednak przekątną. Jakie nie są? – dokładnie boki. Boków mamy  , zatem przekątnych jest
, zatem przekątnych jest
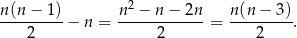
Sposób III
Zadanie można też rozwiązać indukcyjnie.
Trójkąt ma 0 przekątnych, a czworokąt 2.
Zastanówmy się ile tworzy się nowych przekątnych, gdy przechodzimy od 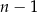 –kąta do
–kąta do  –kąta. Nowe przekątne to te wychodzące z dołożonego wierzchołka. Jest ich dokładnie
–kąta. Nowe przekątne to te wychodzące z dołożonego wierzchołka. Jest ich dokładnie 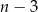 (odrzucamy dwa sąsiednie wierzchołki). Ale to nie wszystko, bo jeszcze odcinek łączący wierzchołki sąsiednie do dołożonego wierzchołka przestaje być bokiem, z zaczyna być przekątną. W sumie jest więc
(odrzucamy dwa sąsiednie wierzchołki). Ale to nie wszystko, bo jeszcze odcinek łączący wierzchołki sąsiednie do dołożonego wierzchołka przestaje być bokiem, z zaczyna być przekątną. W sumie jest więc 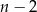 nowych przekątnych. Zatem całkowita liczba przekątnych
nowych przekątnych. Zatem całkowita liczba przekątnych  –kąta jest równa
–kąta jest równa
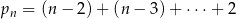
(odejmujemy wierzchołki aż dojdziemy do czworokąta). Sumę tę liczymy ze wzoru na sumę ciągu arytmetycznego.
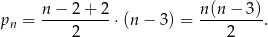
Odpowiedź: