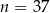Zadanie nr 5522347
Liczba przekątnych  –kąta foremnego jest o 73 mniejsza niż liczba przekątnych
–kąta foremnego jest o 73 mniejsza niż liczba przekątnych 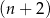 –kąta. Oblicz
–kąta. Oblicz  .
.
Rozwiązanie
Naszkicujmy  –kąt.
–kąt.
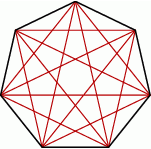
Jeżeli nie pamiętamy gotowego wzoru na liczbę przekątnych  –kąta, to łatwo go wyprowadzić – jest
–kąta, to łatwo go wyprowadzić – jest
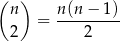
odcinków między wierzchołkami  –kąta, ale wśród nich jest
–kąta, ale wśród nich jest  boków, więc jest
boków, więc jest
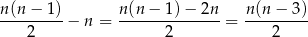
przekątnych.
Pozostało teraz rozwiązać równanie
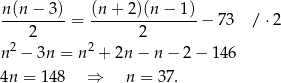
Odpowiedź: