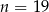Zadanie nr 8152750
W  –kącie foremnym, gdzie
–kącie foremnym, gdzie 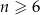 , iloczyn liczby najdłuższych przekątnych przez liczbę najkrótszych przekątnych jest o 342 większy niż liczba osi symetrii tego wielokąta. Oblicz
, iloczyn liczby najdłuższych przekątnych przez liczbę najkrótszych przekątnych jest o 342 większy niż liczba osi symetrii tego wielokąta. Oblicz  .
.
Rozwiązanie
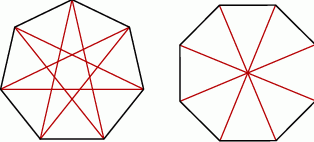
Jeżeli narysujemy kilka wielokątów foremnych, to powinniśmy zauważyć, że  –kąt foremny ma zawsze
–kąt foremny ma zawsze  osi symetrii oraz
osi symetrii oraz  najkrótszych przekątnych (każda taka przekątna odcina jeden wierzchołek)
najkrótszych przekątnych (każda taka przekątna odcina jeden wierzchołek)
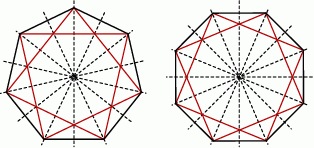
Jeżeli chodzi o liczbę najdłuższych przekątnych, to sprawa jest bardziej skomplikowana – jeżeli  jest parzyste, to jest ich
jest parzyste, to jest ich 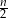 , a jeżeli
, a jeżeli  jest nieparzyste, to jest ich
jest nieparzyste, to jest ich  .
.
Musimy więc rozwiązać dwa równania. Najpierw przypadek  parzystego.
parzystego.
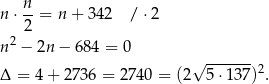
Ponieważ 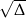 jest niewymierny, równanie to nie ma rozwiązań całkowitych.
jest niewymierny, równanie to nie ma rozwiązań całkowitych.
Teraz przypadek  nieparzystego.
nieparzystego.
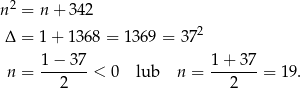
Odpowiedź: