Zadanie nr 1775676
Oblicz 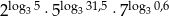 .
.
Rozwiązanie
Sposób I
Oznaczmy
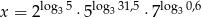
Logarytmujemy teraz to wyrażenie stronami logarytmem przy podstawie 3.
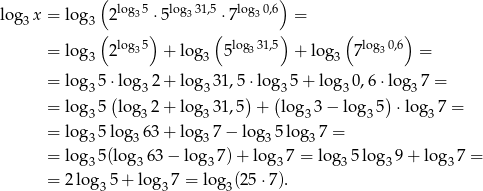
Zatem 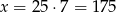 .
.
Sposób II
Zauważmy najpierw, że
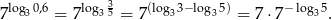
Ponadto
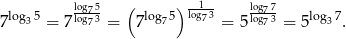
Zatem
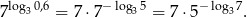
Stąd
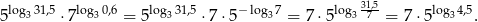
Teraz zauważmy jeszcze, że
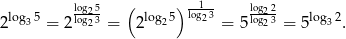
Mamy zatem
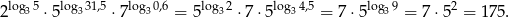
Odpowiedź: 175
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz 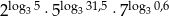 .
.
Sposób I
Oznaczmy
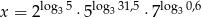
Logarytmujemy teraz to wyrażenie stronami logarytmem przy podstawie 3.
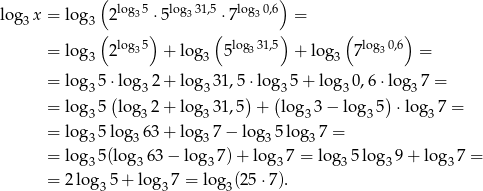
Zatem 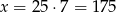 .
.
Sposób II
Zauważmy najpierw, że
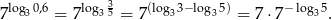
Ponadto
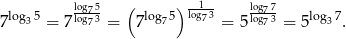
Zatem
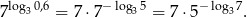
Stąd
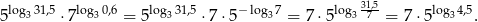
Teraz zauważmy jeszcze, że
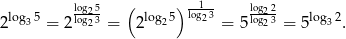
Mamy zatem
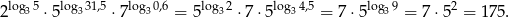
Odpowiedź: 175
