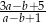/Szkoła średnia/Liczby/Logarytmy/Oblicz

Zadanie nr 4967938

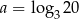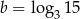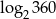Wiedząc, że a = log3 20 i b = log3 15 oblicz lo g2360 .

Wersja PDF

Rozwiązanie

Ponieważ dane logarytmy są przy podstawie 3, na początku zmieniamy podstawę ze wzoru

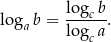
log b = logc-b. a logc a

Liczymy

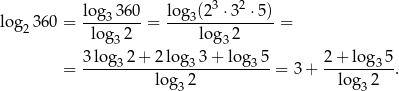
log33-60 log-3(23 ⋅32-⋅5) log 2360 = log 2 = log 2 = 3 3 = 3log-32+--2log-33+--lo-g35-= 3+ 2-+-log35-. lo g32 log3 2

No to widać co mamy obliczyć, popatrzmy teraz na podane założenia.

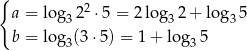
{ a = lo g 22 ⋅5 = 2 lo g 2 + log 5 3 3 3 b = lo g3(3⋅ 5) = 1+ lo g35

Z drugiego równania mamy

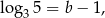
lo g35 = b− 1 ,

a z pierwszego

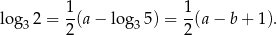
1 1 log32 = -(a − log3 5) = --(a− b + 1 ). 2 2

No i wszystko jasne

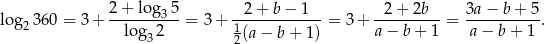
2+ lo g 5 2 + b − 1 2+ 2b 3a − b + 5 lo g236 0 = 3+ -------3--= 3+ 1------------= 3 + --------- = ----------. lo g32 2(a − b + 1) a − b + 1 a− b + 1

 
Odpowiedź: 3a−b+-5 a−b+1

Wersja PDF