Zadanie nr 8371763

Oblicz wartość wyrażenia 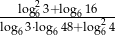log2 3+ log 16 log-36⋅log-486+log2-4 6 6 6 .

Rozwiązanie

Sposób I

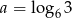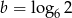Widać, że w podanym wyrażeniu występują różne kombinacje logarytmów a = log 63 i b = log 62 . Używając tych oznaczeń mamy

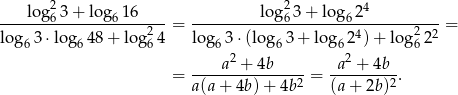
2 2 4 ---log-63+--log61-6---- ---------log6-3+--lo-g62----------- lo g 3 ⋅log 48+ lo g24 = log 3 ⋅(log 3+ lo g 24) + log2 22 = 6 6 6 6 6 6 6 ----a2 +-4b----- -a2 +-4b-- = a(a + 4b) + 4b2 = (a+ 2b)2.

Zanim przekształcimy to wyrażenie dalej, zauważmy, że

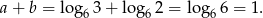
a+ b = log 3+ lo g 2 = log 6 = 1. 6 6 6

Zatem 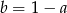b = 1 − a i mamy

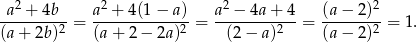
a2 + 4b a2 + 4(1 − a) a2 − 4a+ 4 (a− 2 )2 --------2 = ------------2-= --------2---= -------2 = 1. (a+ 2b ) (a + 2 − 2a) (2 − a) (a− 2 )

Sposób II

Korzystając ze wzoru na zamianę podstawy logarytmu zamieńmy wszystkie logarytmy na dziesiętne.

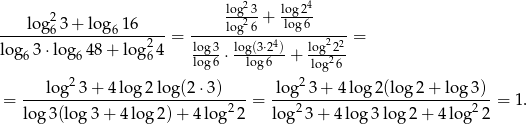
2 2 log-3-+ log24 ----lo-g63-+-log6-16----= -----log26----log-6-----= log 3⋅log 48 + log24 log3 log(3⋅24) log222- 6 6 6 log6 ⋅ log6 + log26 2 2 = ---log--3+--4log-2log-(2⋅3)----= -lo-g-3-+-4-lo-g2(log-2-+-log3-) = 1 . log 3(log3 + 4 log2 )+ 4 log22 log2 3+ 4log 3log 2+ 4log 22

Odpowiedź: 1