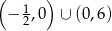/Szkoła średnia/Funkcje/Logarytm/Dziedzina

Zadanie nr 1769568

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz dziedzinę funkcji określonej wzorem 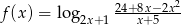24+-8x−2x2 f(x ) = lo g2x+1 x+ 5 .

Rozwiązanie

Podstawa logarytmu musi być dodatnia i nie może być równa 1. Mamy stąd

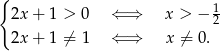
{ 2x+ 1 > 0 ⇐ ⇒ x > − 12 2x+ 1 ⁄= 1 ⇐ ⇒ x ⁄= 0.

Zauważmy teraz, że dla 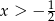1 x > − 2 mianownik logarytmowanego ułamka jest dodatni, więc pozostaje rozwiązać nierówność

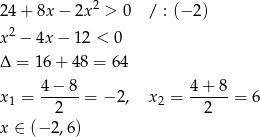
2 24 + 8x − 2x > 0 / : (− 2) x2 − 4x − 1 2 < 0 Δ = 16 + 48 = 6 4 4− 8 4 + 8 x1 = ------= − 2, x2 = ------= 6 2 2 x ∈ (− 2,6)

Dziedziną funkcji 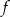f jest więc zbiór

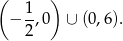
( ) − 1-,0 ∪ (0,6). 2

 
Odpowiedź: ( ) − 1,0 ∪ (0,6) 2

Wersja PDF