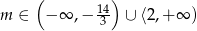/Szkoła średnia/Funkcje/Logarytm/Dziedzina

Zadanie nr 2939774

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 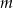m , dla których dziedziną funkcji

2 2 f(x ) = log[(m + m − 6)x + (m − 2)x + 1]

jest zbiór wszystkich liczb rzeczywistych.

Rozwiązanie

Dziedziną loagrytmu jest zbiór liczb dodatnich, zatem pytanie brzmi kiedy wyrażenie 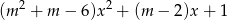(m 2 + m − 6)x2 + (m − 2)x + 1 przyjmuje zawsze (dla dowolnego x ) wartości dodatnie.

Najpierw sprawdźmy kiedy wyrażenie jest liniowe.

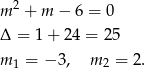
m 2 + m − 6 = 0 Δ = 1+ 24 = 25 m 1 = − 3, m 2 = 2.

Mamy wtedy odpowiednio

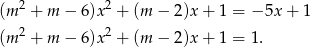
(m2 + m − 6)x2 + (m − 2)x+ 1 = − 5x + 1 2 2 (m + m − 6)x + (m − 2)x+ 1 = 1.

Zatem dla 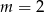m = 2 jest OK, a dla 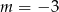m = − 3 jest źle (wyrażenie bywa ujemne).

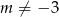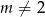Jeżeli m ⁄= − 3 i m ⁄= 2 to mamy funkcję kwadratową. Żeby była zawsze dodatnia, ramiona paraboli będącej jej wykresem muszą być skierowane do góry, czyli

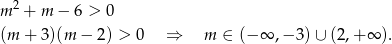
2 m + m − 6 > 0 (m + 3)(m − 2 ) > 0 ⇒ m ∈ (− ∞ ,− 3)∪ (2,+ ∞ ).

Ponadto parabola musi być w całości powyżej osi Ox , czyli Δ < 0 .

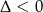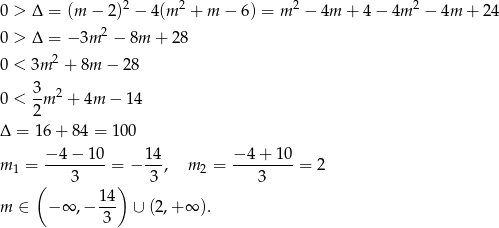
2 2 2 2 0 > Δ = (m − 2) − 4 (m + m − 6) = m − 4m + 4 − 4m − 4m + 24 0 > Δ = − 3m 2 − 8m + 28 2 0 < 3m + 8m − 28 3 2 0 < 2-m + 4m − 14 Δ = 16+ 84 = 100 −-4−--10- 14- −-4+-1-0- m 1 = 3 = − 3 , m 2 = 3 = 2 ( ) m ∈ − ∞ ,− 14- ∪ (2,+ ∞ ). 3

Łącząc wszystkie otrzymane warunki, mamy

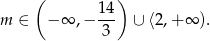
( ) 14 m ∈ − ∞ ,− --- ∪ ⟨2,+ ∞ ). 3

 
Odpowiedź: ( 14) m ∈ − ∞ ,− -3 ∪ ⟨2,+ ∞ )

Wersja PDF