/Szkoła średnia/Funkcje/Logarytm/Dziedzina

Zadanie nr 4508009

Wyznacz te wartości parametru 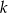k , dla których dziedziną funkcji 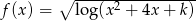∘ ----------------- f (x) = log(x 2 + 4x + k) jest zbiór liczb rzeczywistych.

Wersja PDF

Rozwiązanie

Wyrażenie pod pierwiastkiem musi być nieujemne, a logarytm jest nieujemny, jeżeli jego argument jest 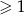≥ 1 . Pytanie zatem brzmi: kiedy nierówność

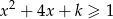
x2 + 4x + k ≥ 1

jest spełniona przez wszystkie liczby rzeczywiste.

Sposób I

Liczymy z 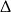Δ -y. Funkcja

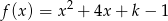
2 f (x) = x + 4x + k − 1

ma nie przyjmować wartości ujemnych, czyli

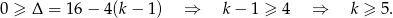
0 ≥ Δ = 16 − 4(k − 1) ⇒ k − 1 ≥ 4 ⇒ k ≥ 5.

Sposób II

Rozważany trójmian kwadratowy łatwo zwinąć do pełnego kwadratu.

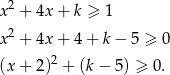
x 2 + 4x + k ≥ 1 2 x + 4x + 4 + k − 5 ≥ 0 (x + 2)2 + (k − 5) ≥ 0.

Widać, że nierówność jest spełniona dla dowolnej liczby rzeczywistej tylko gdy 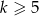k ≥ 5 (żeby to zobaczyć wystarczy podstawić x = − 2 ).  
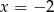Odpowiedź: k ≥ 5

Wersja PDF