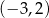/Szkoła średnia/Funkcje/Logarytm/Dziedzina

Zadanie nr 5121682

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz dziedzinę funkcji 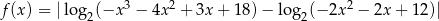3 2 2 f(x) = |lo g2(−x − 4x + 3x + 18) − log2(− 2x − 2x + 12)| .

Rozwiązanie

Wyrażenia w oby logarytmach muszą być dodatnie, więc mamy do rozwiązania dwie nierówności wielomianowe

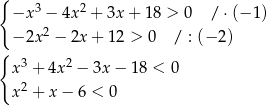
{ −x 3 − 4x 2 + 3x + 18 > 0 / ⋅(− 1) − 2x 2 − 2x + 1 2 > 0 / : (− 2) { x3 + 4x 2 − 3x − 18 < 0 2 x + x − 6 < 0

Rozkładamy najpierw pierwszy wielomian – szukamy pierwiastków całkowitych wśród dzielników wyrazu wolnego – jednym z nich jest 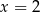x = 2 . Dzielimy ten wielomian przez 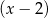(x − 2 ) – zrobimy to grupując wyrazy.

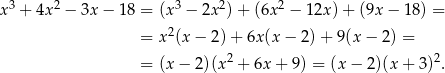
x 3 + 4x 2 − 3x − 18 = (x3 − 2x2) + (6x 2 − 12x )+ (9x − 18) = = x2(x − 2) + 6x (x− 2)+ 9(x− 2) = 2 2 = (x − 2)(x + 6x + 9 ) = (x− 2)(x + 3) .

Rozkładamy jeszcze trójmian z drugiej nierówności

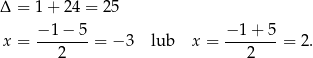
Δ = 1 + 24 = 25 x = −-1-−-5 = − 3 lub x = −-1-+-5 = 2. 2 2

Mamy więc do rozwiązania układ nierówności

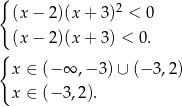
{ 2 (x − 2)(x + 3) < 0 (x − 2)(x + 3) < 0. { x ∈ (− ∞ ,− 3)∪ (−3 ,2) x ∈ (− 3,2).

Rozwiązaniem tego układu nierówności jest przedział 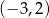(− 3,2) .  
Odpowiedź: (− 3,2)

Wersja PDF