/Szkoła średnia/Funkcje/Logarytm/Dziedzina

Zadanie nr 5457243

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz dziedzinę i najmniejszą wartość funkcji 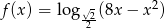√- 2 f(x) = log 22(8x − x ) .

Rozwiązanie

Wyrażenie pod logarytmem musi być dodatnie, więc

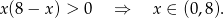
x(8− x) > 0 ⇒ x ∈ (0,8).

Ponieważ 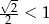√2 2--< 1 więc funkcja 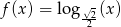f (x) = log√-2(x) 2 jest funkcją malejącą, zatem jej najmniejsza wartość będzie przyjmowana w punkcie, w którym największą wartość przyjmuje funkcja 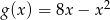2 g(x) = 8x− x , czyli w wierzchołku tej paraboli 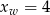xw = 4 . Obliczmy tę wartość

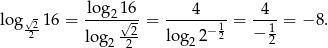
log 16 log √2 16 = ----2√--= ----4----= -4--= − 8. -2 log -2- log2 2− 12 − 12 2 2

Na koniec, dla ciekawskich, wykres podanej funkcji.

PIC

 
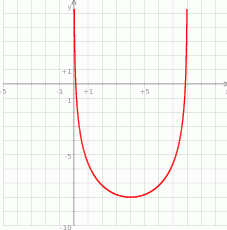
Odpowiedź: Dziedzina: 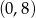(0,8) , wartość najmniejsza: -8

Wersja PDF