/Szkoła średnia/Funkcje/Logarytm/Dziedzina

Zadanie nr 5457720

Wyznacz dziedzinę funkcji 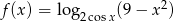2 f(x ) = lo g2cosx(9− x ) i zapisz ją w postaci sumy przedziałów liczbowych.

Wersja PDF

Rozwiązanie

Wyrażenie pod logarytmem musi być dodatnie, czyli

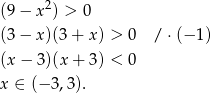
2 (9 − x ) > 0 (3 − x )(3+ x) > 0 / ⋅(− 1) (x − 3)(x+ 3) < 0 x ∈ (− 3,3).

Ponieważ dalej będziemy zajmować się cosinusem zauważmy, że ten przedział zawiera się w przedziale 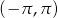(− π,π ) , więc tylko przy takim ograniczeniu będzie nas interesował cosinus.

Podstawa logarytmu musi być dodatnia, czyli

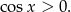
cos x > 0.

Jak już zauważyliśmy interesuje nas tylko przedział 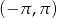(− π,π ) , więc daje to nam

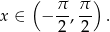
( π π ) x ∈ − --,-- . 2 2

To jeszcze nie koniec, bo podstawa logarytmu nie może być równa 1, czyli

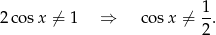
1 2 cosx ⁄= 1 ⇒ co sx ⁄= -. 2

To oznacza, że musimy jeszcze wyrzucić 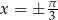π- x = ± 3 .  
Odpowiedź: π- π- π- π- π-π- (− 2 ,− 3) ∪ (− 3, 3)∪ (3, 2)

Wersja PDF