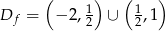Zadanie nr 9704656

Wyznacz dziedzinę funkcji 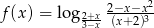2−x-−x2- f(x ) = lo g23+−xx (x+2)3 .

Rozwiązanie

Patrzymy najpierw na podstawę logarytmu – musi być dodatnia i nie może być równa 1. Na początek sprawdźmy, kiedy jest równa 1

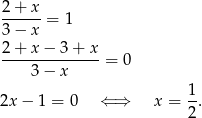
2-+-x-= 1 3 − x 2-+-x-−-3-+-x- 3 − x = 0 1 2x − 1 = 0 ⇐ ⇒ x = -. 2

Zatem 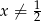1 x ⁄= 2 . Teraz sprawdzamy, kiedy podstawa jest dodatnia.

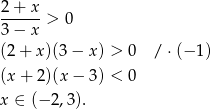
2+ x ------> 0 3− x (2 + x )(3− x) > 0 / ⋅(− 1) (x + 2)(x− 3) < 0 x ∈ (− 2,3).

Wyrażenie pod logarytmem musi być dodatnie i oczywiście mianownik nie może być zerem (czyli 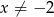x ⁄= − 2 ). Rozłóżmy licznik na czynniki.

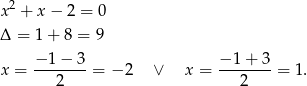
x2 + x − 2 = 0 Δ = 1+ 8 = 9 −-1−-3- −-1+--3 x = 2 = − 2 ∨ x = 2 = 1.

Zatem

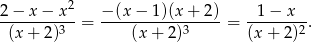
2−--x−--x2- −-(x-−--1)(x+--2)- --1-−-x-- (x+ 2)3 = (x+ 2)3 = (x + 2)2.

Wyrażenie to jest dodatnie jeżeli 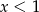x < 1 .

Zbierając teraz wszystkie ograniczenia razem, otrzymujemy dziedzinę:

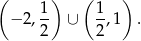
( 1) ( 1 ) − 2,-- ∪ -,1 . 2 2

Odpowiedź: ( ) ( ) Df = − 2, 12 ∪ 12,1