/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą

Zadanie nr 3538089

Dodaj do ulubionych
Dodaj do rozwiązanych

Reszta z dzielenia wielomianu 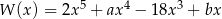5 4 3 W (x) = 2x + ax − 1 8x + bx przez trójmian 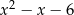x 2 − x − 6 jest równa 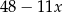48 − 11x . Oblicz resztę z dzielenia wielomianu 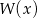W (x) przez trójmian x2 + x− 6 .

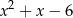Rozwiązanie

Rozłóżmy najpierw trójmian 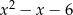2 x − x− 6 na czynniki.

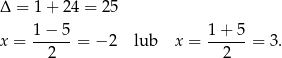
Δ = 1 + 24 = 25 1-−-5- 1-+-5- x = 2 = − 2 lub x = 2 = 3.

Zatem

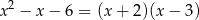
x2 − x − 6 = (x + 2)(x− 3)

i wiemy, że

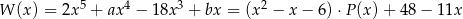
W (x ) = 2x5 + ax4 − 18x 3 + bx = (x2 − x − 6) ⋅P(x) + 48 − 11x

dla pewnego wielomianu 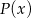P (x) . Podstawiamy w tej równości kolejno 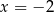x = − 2 i x = 3 .

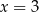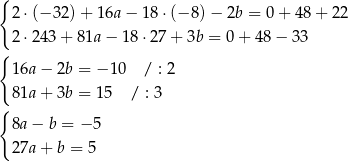
{ 2⋅(− 32 )+ 1 6a− 18⋅(− 8) − 2b = 0+ 48+ 22 2⋅2 43+ 81a− 18 ⋅27+ 3b = 0 + 48 − 33 { 16a − 2b = − 10 / : 2 81a + 3b = 15 / : 3 { 8a− b = − 5 27a + b = 5

Dodajemy te równania stronami i mamy 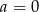a = 0 . Stąd 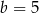b = 5 i

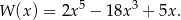
W (x) = 2x5 − 18x 3 + 5x.

Resztę z dzielenia tego wielomianu przez trójmian 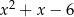x2 + x − 6 wyznaczymy na trzy sposoby.

Sposób I

Zauważmy, że wielomian 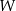W jest funkcją nieparzystą:

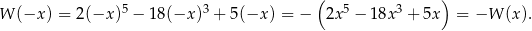
( ) W (−x ) = 2(−x )5 − 18(−x )3 + 5(−x ) = − 2x 5 − 1 8x3 + 5x = −W (x).

Jeżeli więc w równości

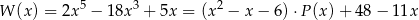
5 3 2 W (x ) = 2x − 18x + 5x = (x − x − 6)⋅ P(x) + 48 − 11x

podstawimy 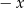− x zamiast x to mamy

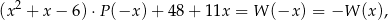
2 (x + x − 6) ⋅P(−x )+ 4 8+ 1 1x = W (−x ) = −W (x),

czyli

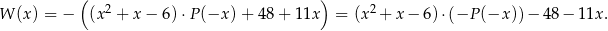
( 2 ) 2 W (x) = − (x + x − 6) ⋅P(−x )+ 4 8+ 11x = (x + x − 6) ⋅(−P (−x ))− 48− 11x.

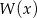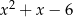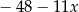To oznacza, że reszta z dzielenia wielomianu W (x) przez trójmian 2 x + x − 6 jest równa − 48 − 11x .

Sposób II

Rozłóżmy trójmian 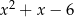2 x + x − 6 na czynniki.

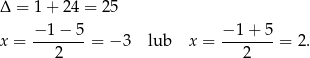
Δ = 1 + 24 = 25 x = −-1-−-5 = − 3 lub x = −-1-+-5 = 2. 2 2

Zatem

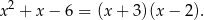
2 x + x − 6 = (x + 3)(x − 2 ).

Reszta z dzielenia wielomianu 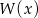W (x ) przez ten trójmian jest wielomianem stopnia 1, czyli jest postaci px + q :

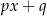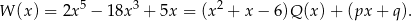
W (x) = 2x 5 − 1 8x3 + 5x = (x 2 + x − 6)Q (x )+ (px + q).

Podstawiamy w tej równości kolejno: 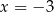x = − 3 i x = 2 .

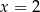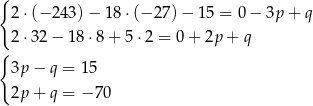
{ 2 ⋅(− 243) − 18 ⋅(− 27)− 15 = 0 − 3p + q 2 ⋅32 − 18 ⋅8+ 5⋅ 2 = 0+ 2p + q { 3p − q = 15 2p + q = − 70

Dodajemy równania stronami i mamy 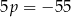5p = −5 5 , czyli 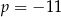p = − 11 . Stąd 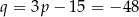q = 3p− 15 = − 48 i interesująca nas reszta jest równa

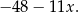
− 48 − 1 1x.

Sposób III

Dzielimy wielomian

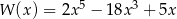
5 3 W (x) = 2x − 18x + 5x

przez trójmian 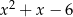2 x + x − 6 – my zrobimy to grupując wyrazy.

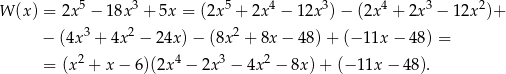
5 3 5 4 3 4 3 2 W (x ) = 2x − 18x + 5x = (2x + 2x − 12x ) − (2x + 2x − 12x )+ − (4x 3 + 4x 2 − 24x) − (8x2 + 8x − 48 )+ (− 11x − 48) = = (x2 + x− 6)(2x4 − 2x3 − 4x 2 − 8x )+ (− 11x − 48).

Interesująca nas reszta jest więc równa

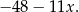
− 48 − 1 1x.

 
Odpowiedź: − 48 − 11x

Wersja PDF