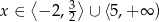/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą

Zadanie nr 3696777

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian określony wzorem 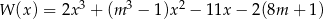3 3 2 W (x) = 2x + (m − 1)x − 11x − 2(8m + 1) jest podzielny przez dwumian 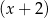(x+ 2) oraz przy dzieleniu przez dwumian 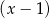(x − 1) daje resztę 12. Oblicz 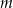m i dla wyznaczonej wartości 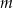m rozwiąż nierówność W (x) ≥ 0 .

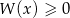Rozwiązanie

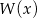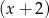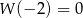Jeżeli wielomian W (x) dzieli się przez (x + 2) , to W (− 2) = 0 . Podobnie, jeżeli jego reszta z dzielenia przez 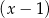(x − 1) jest równa 12, to 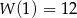W (1) = 12 (wynika to natychmiast z dzielnia z resztą: 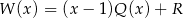W (x) = (x − 1)Q (x) + R ). Mamy zatem układ równań

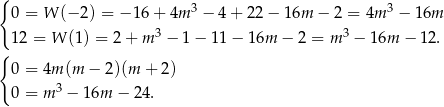
{ 0 = W (− 2) = − 16+ 4m 3 − 4+ 2 2− 16m − 2 = 4m 3 − 16m 3 3 12 = W (1) = 2 + m − 1− 11− 16m − 2 = m − 1 6m − 12 . { 0 = 4m (m − 2)(m + 2) 0 = m 3 − 16m − 24.

Z pierwszego równania mamy 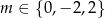m ∈ {0,− 2,2 } . Łatwo sprawdzić, że spośród tych liczb tylko 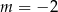m = − 2 spełnia drugie równanie. Zatem

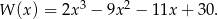
W (x) = 2x3 − 9x2 − 11x + 30.

Wiemy ponadto, że wielomian ten dzieli się przez 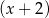(x+ 2) . Wykonujemy to dzielenie – my zrobimy to grupując wyrazy.

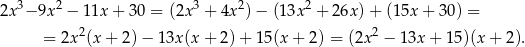
2x3− 9x2 − 11x + 30 = (2x3 + 4x 2) − (13x 2 + 26x) + (15x + 30) = 2 2 = 2x (x+ 2)− 13x(x + 2) + 15(x + 2 ) = (2x − 13x + 15)(x + 2 ).

Rozkładamy jeszcze trójmian w pierwszym nawiasie.

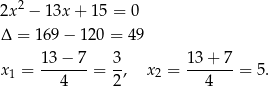
2 2x − 13x + 15 = 0 Δ = 16 9− 1 20 = 49 13 − 7 3 13 + 7 x 1 = -------= -, x2 = -------= 5. 4 2 4

Mamy zatem

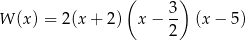
( 3 ) W (x) = 2(x+ 2) x − -- (x − 5) 2

i rozwiązaniem nierówności 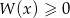W (x ) ≥ 0 jest zbiór

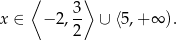
⟨ 3⟩ x ∈ − 2,-- ∪ ⟨5,+ ∞ ). 2

PIC

 
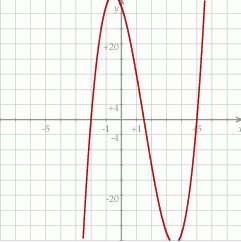
Odpowiedź: 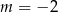m = − 2 , ⟨ ⟩ x ∈ − 2, 32 ∪ ⟨5,+ ∞ )

Wersja PDF