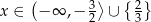/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą

Zadanie nr 5843010

Dodaj do ulubionych
Dodaj do rozwiązanych

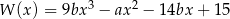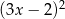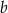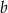Reszta z dzielenia wielomianu 3 2 W (x) = 9bx − ax − 14bx + 15 przez trójmian (3x − 2 )2 wynosi 3. Oblicz a i b . Dla wyznaczonych wartości a i b rozwiąż nierówność W (x) ≤ 3 .

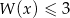Rozwiązanie

Wiemy, że

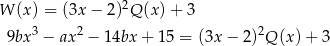
2 W (x ) = (3x − 2) Q (x) + 3 9bx 3 − ax 2 − 14bx + 15 = (3x − 2)2Q (x)+ 3

dla pewnego wielomianu 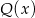Q (x) . Podstawiamy w tej równości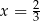 x = 2 3

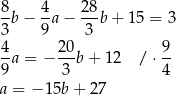
8- 4- 28- 3b − 9a− 3 b+ 1 5 = 3 4 20 9 -a = − --b + 12 / ⋅-- 9 3 4 a = − 15b + 27

Mamy zatem

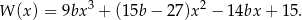
W (x ) = 9bx3 + (15b − 27 )x 2 − 14bx + 15.

Sposób I

Jak zauważyliśmy wyżej

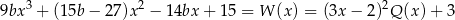
3 2 2 9bx + (15b − 27)x − 1 4bx+ 15 = W (x) = (3x − 2) Q (x) + 3

dla pewnego wielomianu 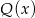Q (x) . Liczymy pochodną obu stron (różniczkujemy stronami).

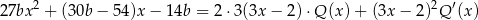
2 2 ′ 27bx + (30b − 5 4)x− 14b = 2 ⋅3(3x − 2 )⋅Q (x) + (3x − 2) Q (x)

Podstawiamy teraz w tej równości 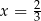x = 23 .

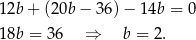
1 2b+ (20b− 36)− 14b = 0 1 8b = 36 ⇒ b = 2.

Stąd 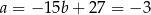a = − 15b + 27 = − 3 i

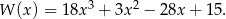
3 2 W (x) = 18x + 3x − 2 8x+ 15.

Pozostało rozwiązać nierówność

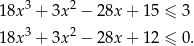
18x3 + 3x2 − 28x + 15 ≤ 3 18x3 + 3x2 − 28x + 12 ≤ 0.

Zauważmy jeszcze, że z treści zadania wynika, że lewa strona dzieli się przez 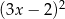(3x − 2 )2 . Wykonujemy to dzielenie – można od razu dzielić przez 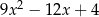2 9x − 1 2x+ 4 , ale my zamiast tego dwa razy podzielimy przez (3x − 2) . Jak zwykle zrobimy to grupując wyrazy.

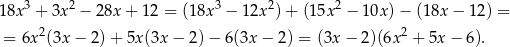
3 2 3 2 2 18x + 3x − 28x + 1 2 = (18x − 12x )+ (1 5x − 10x) − (18x − 1 2) = = 6x2(3x − 2 )+ 5x (3x − 2)− 6(3x − 2) = (3x − 2)(6x2 + 5x − 6).

Dzielimy teraz wielomian w drugim nawiasie przez 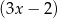(3x − 2) .

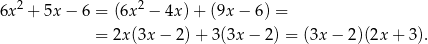
2 2 6x + 5x− 6 = (6x − 4x )+ (9x − 6) = = 2x (3x− 2)+ 3(3x − 2) = (3x − 2 )(2x+ 3).

Musimy więc rozwiązać nierówność

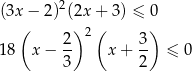
2 (3x − 2) (2x + 3) ≤ 0 ( 2 )2 ( 3) 18 x − -- x+ -- ≤ 0 3 2

Szkicujemy teraz wielomian stopnia 3.

PIC

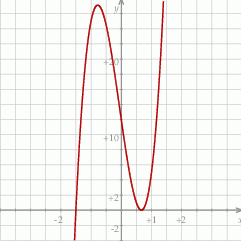
Z wykresu odczytujemy rozwiązanie nierówności.

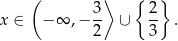
( 3⟩ { 2 } x ∈ −∞ ,− -- ∪ -- . 2 3

Sposób II

Jak już zauważyliśmy,

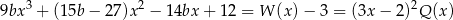
9bx3 + (15b − 27)x 2 − 1 4bx+ 12 = W (x)− 3 = (3x − 2)2Q (x)

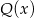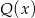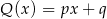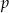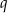dla pewnego wielomianu Q (x) . Ponieważ z lewej strony mamy wielomian stopnia 3, wielomian Q (x) musi być wielomianem liniowym, czyli Q (x) = px + q dla pewnych p i q . Mamy zatem

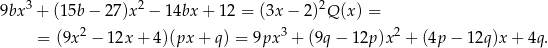
9bx3 + (15b − 27 )x2 − 14bx + 12 = (3x − 2)2Q (x) = = (9x 2 − 12x + 4)(px + q ) = 9px3 + (9q − 12p )x2 + (4p − 12q)x + 4q.

Porównujemy wyrazy wolne po obu stronach i mamy 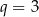q = 3 . Porównujemy współczynniki przy 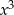3 x i mamy 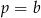p = b . Powyższa równość przyjmuje więc postać

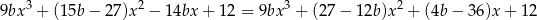
9bx3 + (15b − 2 7)x2 − 14bx + 12 = 9bx3 + (27 − 12b)x 2 + (4b − 3 6)x+ 12

Porównujemy teraz współczynniki przy 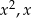2 x ,x i mamy

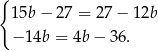
{ 15b− 27 = 27 − 12b −1 4b = 4b − 36.

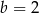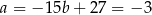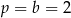Każde z równań jest spełnione tylko przez b = 2 . Mamy wtedy a = −1 5b+ 27 = − 3 oraz p = b = 2 . To oznacza, że

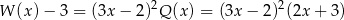
2 2 W (x )− 3 = (3x − 2) Q (x) = (3x − 2 ) (2x + 3)

i pozostało rozwiązać nierówność

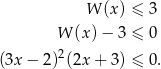
W (x) ≤ 3 W (x) − 3 ≤ 0 2 (3x − 2) (2x + 3) ≤ 0 .

Nierówność tę rozwiązujemy tak samo jak w pierwszym sposobie.

Sposób III

Jak już zauważyliśmy,

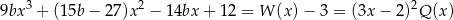
9bx3 + (15b − 27)x 2 − 1 4bx+ 12 = W (x)− 3 = (3x − 2)2Q (x)

dla pewnego wielomianu 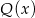Q (x) . Dzielimy więc lewą stronę przez 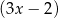(3x − 2) – my zrobimy to grupując wyrazy.

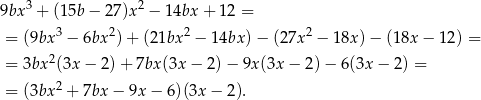
9bx3 + (15b − 27 )x2 − 14bx + 12 = 3 2 2 2 = (9bx − 6bx )+ (2 1bx − 14bx )− (27x − 18x) − (18x − 12 ) = = 3bx 2(3x − 2)+ 7bx(3x − 2) − 9x (3x− 2)− 6(3x − 2) = = (3bx 2 + 7bx − 9x− 6)(3x − 2).

Mamy zatem

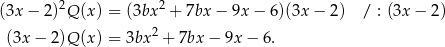
2 2 (3x − 2) Q (x) = (3bx + 7bx − 9x − 6 )(3x− 2) / : (3x − 2) (3x − 2)Q (x) = 3bx2 + 7bx − 9x − 6 .

Podstawiamy teraz w tej równości 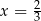2 x = 3 .

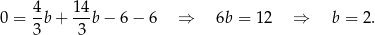
4 14 0 = -b + ---b− 6− 6 ⇒ 6b = 12 ⇒ b = 2. 3 3

Stąd 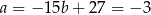a = − 15b + 27 = − 3 oraz

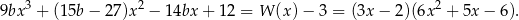
3 2 2 9bx + (1 5b− 27)x − 14bx + 12 = W (x) − 3 = (3x − 2)(6x + 5x − 6).

Rozkładamy jeszcze trójmian w nawiasie.

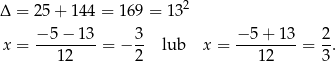
Δ = 25+ 144 = 16 9 = 132 − 5− 13 3 − 5 + 13 2 x = ---------= − -- lub x = ---------= --. 12 2 12 3

Stąd

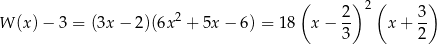
( ) 2( ) W (x)− 3 = (3x − 2)(6x 2 + 5x− 6) = 18 x− 2- x + 3- 3 2

i pozostało rozwiązać nierówność

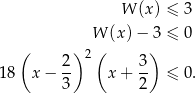
W (x ) ≤ 3 W (x)− 3 ≤ 0 ( ) 2 ( ) 1 8 x − 2- x + 3- ≤ 0. 3 2

Nierówność tę rozwiązujemy tak samo jak w pierwszym sposobie.  
Odpowiedź: 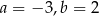a = − 3,b = 2 , x ∈ (− ∞ ,− 3⟩ ∪ { 2} 2 3

Wersja PDF