/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą

Zadanie nr 7008201

Dla jakich wartości 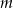m reszta z dzielenia wielomianu 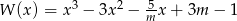3 2 5- W (x ) = x − 3x − m x + 3m − 1 przez dwumian 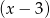(x − 3) jest niewiększa od 3?

Wersja PDF

Rozwiązanie

Oczywiście musi być 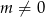m ⁄= 0 . Reszta z dzielenia wielomianu 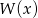W (x) przez dwumian 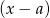(x − a) to po prostu 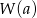W (a) (jeżeli ktoś tego nie wie, to polecam lekturę poradnika). Musimy więc rozwiązać nierówność

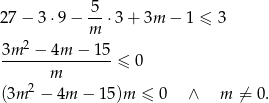
5- 27− 3⋅9 − m ⋅3 + 3m − 1 ≤ 3 2 3m--−--4m-−-15-≤ 0 m (3m 2 − 4m − 15)m ≤ 0 ∧ m ⁄= 0.

Rozkładamy trójmian w nawiasie.

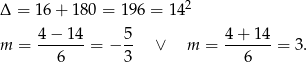
Δ = 16+ 180 = 1 96 = 142 m = 4-−-14-= − 5- ∨ m = 4+--14-= 3. 6 3 6

Mamy zatem nierówność

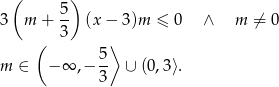
( 5) 3 m + -- (x − 3)m ≤ 0 ∧ m ⁄= 0 ( 3 ⟩ 5 m ∈ − ∞ ,− -- ∪ (0,3⟩. 3

 
Odpowiedź: ( 5⟩ m ∈ − ∞ ,− 3 ∪ (0,3⟩

Wersja PDF