Zadanie nr 7253604
Wiedząc, że wielomian 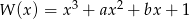 jest podzielny przez wielomian
jest podzielny przez wielomian 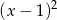 , oblicz
, oblicz  i
i 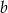 .
.
Rozwiązanie
Sposób I
Dzielimy 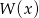 przez
przez 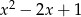 nie przejmując się parametrami. My zrobimy to grupując wyrazy.
nie przejmując się parametrami. My zrobimy to grupując wyrazy.
![3 2 3 2 2 W (x) = x + ax[ + bx+ 1 = (x − 2x + x )+ (a]+ 2)x + (b − 1)x + 1 = = x(x − 1)2 + (a + 2)x 2 − 2(a + 2)x + (a+ 2 ) + (b − 1 + 2a + 4 )x + 1− a − 2 = = x(x − 1)2 + (a + 2)(x − 1)2 + (b + 2a + 3)x − a − 1.](https://img.zadania.info/zad/7253604/HzadR2x.gif)
Otrzymany wielomian liniowy jest resztą dzielenia i zgodnie z założeniem musi być zerowy. Stąd
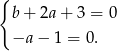
Z drugiego równania mamy 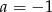 , co w połączeniu z pierwszym daje
, co w połączeniu z pierwszym daje 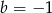 .
.
Sposób II
Tym razem będziemy bardziej ’szkolni’. Sprawdzamy kiedy 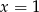 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 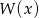 .
.
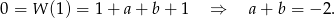
Dzielimy teraz 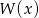 przez
przez 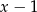 . Najłatwiej to zrobić schematem Hornera, ale my będziemy grupować wyrazy.
. Najłatwiej to zrobić schematem Hornera, ale my będziemy grupować wyrazy.
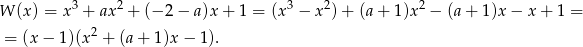
Trójmian w nawiasie też musi się dzielić przez 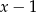 , czyli
, czyli 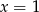 musi być jego miejscem zerowym. Daje nam to
musi być jego miejscem zerowym. Daje nam to
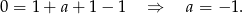
Stąd 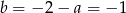 .
.
Sposób III
Zadanie można bardzo łatwo rozwiązać używając pochodnych. Łatwo zauważyć, że jeżeli jakaś liczba jest pierwiastkiem podwójnym wielomianu, to jest też pierwiastkiem jego pochodnej. Tak jak poprzednio zauważamy, że 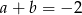 . Drugie równanie dostaniemy z faktu, że
. Drugie równanie dostaniemy z faktu, że 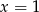 jest pierwiastkiem pochodnej.
jest pierwiastkiem pochodnej.
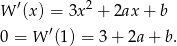
Mamy zatem układ równań
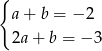
Odejmując od drugiego równania pierwsze, mamy 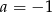 , stąd
, stąd 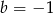 .
.
Sposób IV
Bardzo proste rozwiązanie otrzymamy jeżeli skorzystamy ze wzorów Viète’a dla wielomianów stopnia 3. Wiemy, że wielomian ma mieć dwa pierwiastki równe 1, a ze wzorów Viète’a mamy
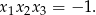
Zatem trzeci pierwiastek musi być równy -1 i mamy
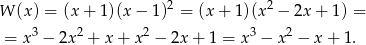
Więcej o wzorach Viète’a można poczytać w poradniku.
Sposób V
Wiemy, że wielomian 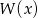 musi mieć postać
musi mieć postać
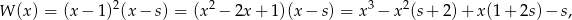
dla pewnego  . Mamy więc równość
. Mamy więc równość
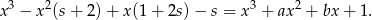
Porównując wyrazy wolne mamy 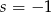 . Wtedy porównując współczynniki przy
. Wtedy porównując współczynniki przy 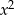 i
i  mamy
mamy 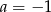 i
i 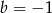 .
.
Odpowiedź: