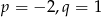/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą

Zadanie nr 8212153

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 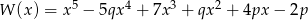5 4 3 2 W (x) = x − 5qx + 7x + qx + 4px − 2p jest podzielny przez wielomian 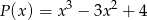P(x) = x 3 − 3x 2 + 4 . Wyznacz 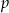p i q .

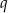Rozwiązanie

Sposób I

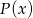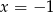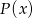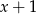Rozłóżmy wielomian P(x ) na czynniki. Szukamy najpierw jakiegoś pierwiastka wymiernego – sprawdzając dzielniki wyrazu wolnego łatwo zauważyć, że pierwiastkiem jest np. x = −1 . Dzielimy zatem P(x) przez x + 1 . My zrobimy to grupując wyrazy.

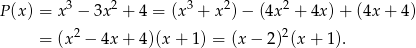
3 2 3 2 2 P (x) = x − 3x + 4 = (x + x )− (4x + 4x) + (4x + 4) = (x 2 − 4x + 4)(x+ 1) = (x − 2)2(x + 1).

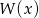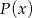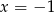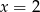Widać zatem, że jeżeli wielomian W (x ) jest podzielny przez P (x) to liczby x = − 1 i x = 2 muszą być pierwiastkami wielomianu 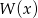W (x ) . Otrzymujemy zatem układ równań

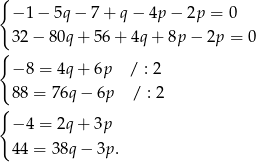
{ − 1 − 5q − 7 + q − 4p − 2p = 0 32 − 80q + 5 6+ 4q + 8p− 2p = 0 { − 8 = 4q + 6p / : 2 88 = 76q− 6p / : 2 { − 4 = 2q + 3p 44 = 38q− 3p.

Dodając równania stronami (żeby wyredukować 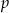p ) mamy 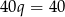4 0q = 40 , czyli q = 1 .

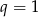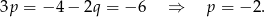
3p = − 4 − 2q = − 6 ⇒ p = − 2 .

Sposób II

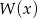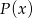Dzielimy wielomian W (x ) przez P(x) nie przejmując się parametrami. My zrobimy to grupując wyrazy.

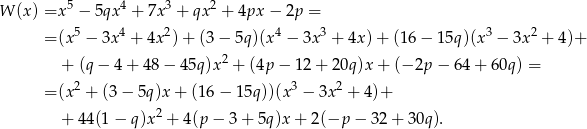
5 4 3 2 W (x) =x − 5qx + 7x + qx + 4px − 2p = = (x5 − 3x4 + 4x2) + (3 − 5q)(x 4 − 3x 3 + 4x )+ (16− 15q)(x3 − 3x2 + 4)+ 2 + (q− 4+ 4 8− 45q)x + (4p − 12 + 20q )x+ (− 2p − 64 + 60q) = = (x2 + (3− 5q)x + (16 − 15q ))(x 3 − 3x 2 + 4)+ + 44(1 − q)x2 + 4(p − 3 + 5q)x + 2 (−p − 32+ 30q).

Skoro 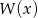W (x) ma się dzielić przez 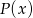P (x) otrzymana reszta musi być wielomianem zerowym. Otrzymujemy stąd układ równań

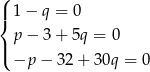
( |{ 1− q = 0 p− 3+ 5q = 0 |( −p − 32+ 30q = 0

Z pierwszego równania mamy 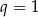q = 1 . Wtedy z drugiego równania 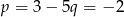p = 3− 5q = − 2 . Łatwo sprawdzić, że liczby te spełniają też trzecie równanie.  
Odpowiedź: p = − 2,q = 1

Wersja PDF