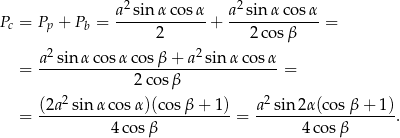/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworościan

Zadanie nr 1371678

Dodaj do ulubionych
Dodaj do rozwiązanych

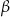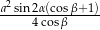Podstawą ostrosłupa jest trójkąt prostokątny o kącie ostrym α i przeciwprostokątnej długości a . Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem β . Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe a2sin2α(cosβ+-1) 4cosβ .

Rozwiązanie

Rozpoczynamy oczywiście od dużego rysunku.

PIC

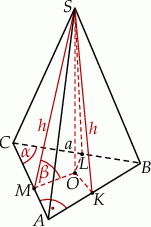
Na rysunku narysowaliśmy wysokości ścian bocznych, żeby móc zaznaczyć kąty nachylenia tych ścian do płaszczyzny podstawy. Ponieważ wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem, trójkąty prostokątne 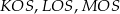KOS ,LOS ,MOS są przystające, czyli 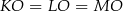KO = LO = MO , co oznacza, że spodek wysokości 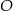O jest środkiem okręgu wpisanego w trójkąt 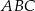ABC . W takim razie do wyliczenia wysokości ścian bocznych brakuje nam długości promienia okręgu wpisanego w trójkąt 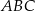ABC . Obliczmy najpierw boki tego trójkąta

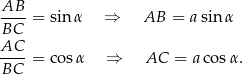
AB-- BC = sin α ⇒ AB = a sinα AC ---- = cos α ⇒ AC = aco sα. BC

Korzystamy teraz z gotowego wzoru na promień r okręgu wpisanego w trójkąt prostokątny:

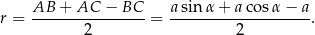
AB + AC − BC asin α+ acos α− a r = ----------------= -------------------. 2 2

To pozwala nam obliczyć wysokość 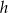h ściany bocznej

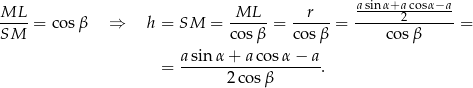
asinα+a-cosα−a-- ML-- = cosβ ⇒ h = SM = -ML-- = --r-- = -------2------ = SM cos β cosβ cosβ a sin α + a cosα − a = --------------------. 2cos β

Liczymy teraz pole powierzchni całkowitej ostrosłupa

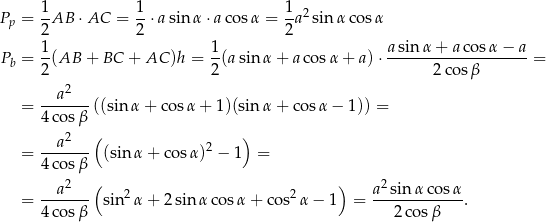
1 1 1 2 Pp = 2AB ⋅AC = 2-⋅asin α⋅a cosα = 2-a sinα cos α Pb = 1(AB + BC + AC )h = 1(a sin α + a cosα + a) ⋅ a-sin-α-+-a-cosα-−-a-= 2 2 2cos β a2 = -------((sin α + cos α+ 1)(sin α + co sα − 1)) = 4cos β a2 ( 2 ) = ------- (sinα + c osα) − 1 = 4cos β --a2---( 2 2 ) a2-sin-α-cosα- = 4cos β sin α + 2 sinα cos α+ cos α − 1 = 2 cosβ .

Stąd

2 2 P = P + P = a--sin-α-cosα-+ a-sin-αco-sα-= c p b 2 2co sβ 2 2 = a-sin-αco-sα-cosβ-+-a--sin-α-cosα-= 2c osβ (2a2sin αco sα)(cos β + 1) a2sin 2α(cos β+ 1) = ---------------------------= -------------------. 4co sβ 4 cosβ
Wersja PDF