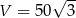/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworościan

Zadanie nr 6673996

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa 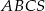ABCS jest trójkąt równoramienny ABC , w którym 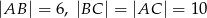|AB | = 6, |BC | = |AC | = 10 , a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt 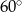60∘ . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

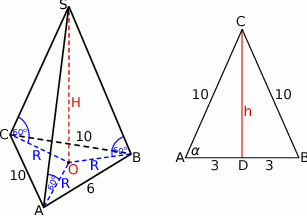
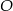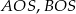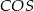Niech O będzie spodkiem wysokości ostrosłupa. Ponieważ trójkąty AOS ,BOS i COS są prostopadłe do płaszczyzny podstawy, ich kąty 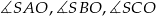∡SAO ,∡SBO ,∡SCO są równe kątom nachylenia krawędzi bocznych do płaszczyzny podstawy. Każdy z tych kątów jest więc równy 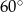∘ 60 . To z kolei oznacza, że trójkąty prostokątne 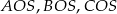AOS ,BOS ,COS są przystające, więc w szczególności

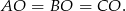
AO = BO = CO .

Uzasadniliśmy więc, że spodek O wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie. To pozwoli nam obliczyć wysokość ostrosłupa, jeżeli tylko będziemy znali długość promienia okręgu opisanego na trójkącie ABC .

Zajmijmy się więc trójkątem w podstawie. Korzystając z twierdzenia Pitagorasa obliczamy długość jego wysokości

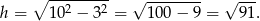
∘ --------- √ -------- √ --- h = 102 − 32 = 10 0− 9 = 91.

Pole tego trójkąta jest więc równe

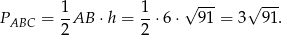
√ --- √ --- PABC = 1AB ⋅h = 1-⋅6 ⋅ 91 = 3 9 1. 2 2

Teraz z twierdzenia sinusów obliczamy promień okręgu opisanego na trójkącie ABC .

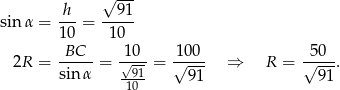
√ --- sin α = h--= --91- 10 10 -BC-- -10- -100- -50-- 2R = sin α = √-91 = √ 9-1 ⇒ R = √ 91-. 10

Obliczamy teraz wysokość ostrosłupa – patrzymy na trójkąt prostokątny AOS .

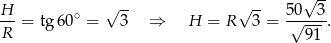
√ -- H- ∘ √ -- √ -- 5-0--3 R = tg60 = 3 ⇒ H = R 3 = √ 91-.

Pozostało obliczyć objętość ostrosłupa.

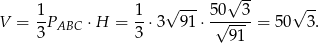
√ -- 1 1 √ --- 50 3 √ -- V = --PABC ⋅H = -⋅ 3 91 ⋅-√----= 50 3. 3 3 91

 
Odpowiedź: √ -- V = 50 3

Wersja PDF