/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworościan

Zadanie nr 7842445

Dodaj do ulubionych
Dodaj do rozwiązanych

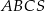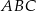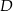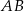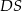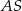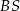Podstawą ostrosłupa ABCS jest trójkąt równoboczny ABC o boku długości 6. Punkt D jest środkiem krawędzi AB , odcinek DS jest wysokością ostrosłupa. Krawędzie AS i BS mają długość 8. Oblicz długość krawędzi 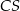CS tego ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku.

PIC

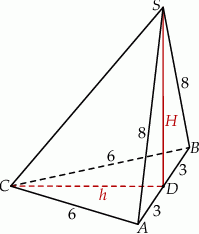
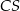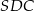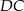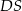Widać, że długość krawędzi CS ostrosłupa można obliczyć z trójkąta prostokątnego SDC , ale najpierw musimy obliczyć długości odcinków DC i DS . Pierwszy z nich to po prostu wysokość w trójkącie równobocznym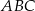 ABC

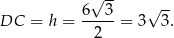
-- 6√ 3 √ -- DC = h = -----= 3 3. 2

Długość drugiego obliczamy z trójkąta 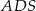ADS

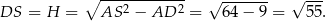
∘ ----2------2 √ ------- √ --- DS = H = AS − AD = 64 − 9 = 55.

Możemy teraz obliczyć długość odcinka 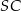SC .

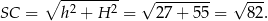
∘ -2-----2 √ -------- √ --- SC = h + H = 27 + 55 = 82.

 
Odpowiedź: √ --- 82

Wersja PDF