/Szkoła średnia/Geometria/Stereometria/Ostrosłup

Zadanie nr 1066525

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa jest romb, którego przekątne mają długości 12 i 16. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych rombu w podstawie, a pole powierzchni bocznej jest równe 104. Oblicz objętość ostrosłupa.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

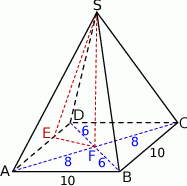
Niech 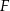F będzie punktem przecięcia przekątnych rombu. Ponieważ przekątne rombu dzielą się na połowy i są prostopadłe, trójkąt 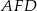AF D jest prostokątny oraz

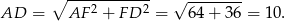
∘ ------------ √ -------- AD = AF 2 + FD 2 = 64 + 36 = 10.

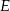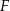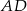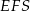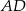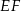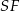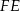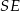Niech E będzie rzutem punktu F na krawędź AD . Płaszczyzna EF S jest prostopadła do prostej AD (bo zawiera dwie proste: EF i SF prostopadłe do tej krawędzi), więc odcinki F E i SE są wysokościami odpowiednio w trójkątach 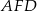AF D i ADS .

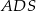Długość odcinka 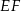EF możemy wyliczyć porównując dwa wzory na pole trójkąta prostokątnego AF D .

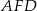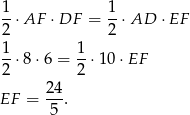
1- 1- 2 ⋅AF ⋅DF = 2 ⋅AD ⋅EF 1 1 --⋅8 ⋅6 = --⋅1 0⋅EF 2 2 EF = 24-. 5

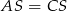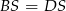Ponieważ ściany boczne są przystające (bo AS = CS i BS = DS ), z podanego pola powierzchni bocznej możemy obliczyć długość wysokości 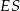ES ściany bocznej

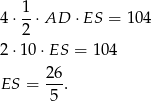
1 4⋅ -⋅ AD ⋅ES = 104 2 2⋅1 0⋅ES = 10 4 26 ES = --. 5

Teraz z trójkąta prostokątnego 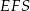EF S obliczamy wysokość ostrosłupa SF .

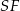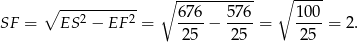
∘ ----------- ∘ ----------- ∘ ---- SF = ES 2 − EF 2 = 676-− 576-= 100-= 2. 2 5 25 25

Pozostało obliczyć objętość.

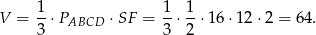
1 1 1 V = --⋅PABCD ⋅SF = -⋅ --⋅16 ⋅12⋅ 2 = 64. 3 3 2

 
Odpowiedź: 64

Wersja PDF