/Szkoła średnia/Geometria/Stereometria/Ostrosłup

Zadanie nr 1688979

Udowodnij, że suma długości wysokości ścian bocznych ostrosłupa pięciokątnego jest nie większa niż suma długości jego krawędzi bocznych.

Wersja PDF

Rozwiązanie

Samo zadanie jest dość proste, ale ponieważ w podstawie mamy pięciokąt, trzeba w przemyślany sposób wszystko pooznaczać, żeby móc łatwo zapisać uzasadnienie.

PIC

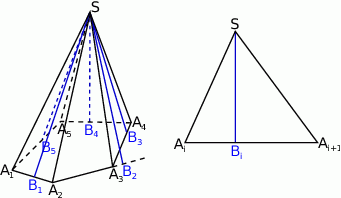
Powiedzmy, że w podstawie jest pięciokąt 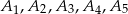A1,A 2,A 3,A 4,A5 , wierzchołek niech będzie punktem 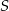S , a spodki wysokości ścian bocznych na proste zawierające krawędzie
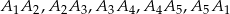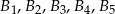A 1A 2,A 2A3,A 3A 4,A 4A5,A 5A 1 oznaczmy przez B1,B2,B 3,B4,B5 .

Zauważmy teraz, że w trójkącie o wierzchołkach 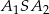A1SA 2 wysokość 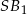SB 1 jest nie dłuższa niż długość odcinka 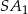SA 1 – tak jest, bo 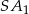SA 1 jest przeciwprostokątną w trójkącie prostokątnym 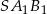SA 1B 1 (odcinki te mogą mieć takie same długości dokładnie w jednym przypadku: gdy 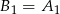B = A 1 1 ). Mamy zatem

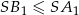
SB 1 ≤ SA 1

Analogicznie uzasadniamy, że

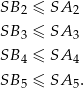
SB ≤ SA 2 2 SB 3 ≤ SA 3 SB ≤ SA 4 4 SB 5 ≤ SA 5.

Dodając te pięć nierówności stronami otrzymujemy

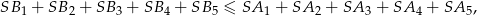
SB 1 + SB 2 + SB 3 + SB 4 + SB 5 ≤ SA 1 + SA 2 + SA 3 + SA 4 + SA 5,

czyli dokładnie nierówność którą mieliśmy wykazać.

Wersja PDF