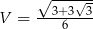/Szkoła średnia/Geometria/Stereometria/Ostrosłup

Zadanie nr 2192965

Dodaj do ulubionych
Dodaj do rozwiązanych

Wszystkie krawędzie boczne ostrosłupa trójkątnego 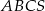ABCS o wierzchołku 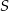S mają długość 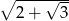∘ ----√--- 2+ 3 . Wiedząc, że 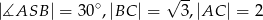√ -- |∡ASB | = 30∘,|BC | = 3,|AC | = 2 oblicz objętość tego ostrosłupa.

Rozwiązanie

Rozpoczynamy oczywiście od dużego rysunku.

PIC

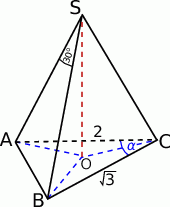
Popatrzmy najpierw co jest grane. Ponieważ wszystkie krawędzie boczne mają równą długość, trójkąty prostokątne 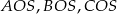AOS ,BOS ,COS są przystające, czyli 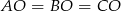AO = BO = CO , co oznacza, że spodek wysokości 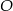O jest środkiem okręgu opisanego na trójkącie 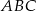ABC . W takim razie do wyliczenia długości wysokości 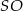SO ostrosłupa brakuje nam długości promienia okręgu opisanego na trójkącie 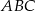ABC (bo wtedy zastosujemy twierdzenie Pitagorasa do trójkąta 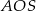AOS ). Długość promienia okręgu opisanego będziemy mogli wyliczyć z twierdzenia sinusów, jeżeli będziemy np. znali długość odcinka 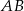AB i miarę kąta 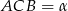ACB = α . Mając miarę tego kąta łatwo też będzie obliczyć pole trójkąta w podstawie. Rozwiązanie sprowadziliśmy więc do wyliczenia długości odcinka 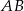AB i kąta α .

Długość odcinka 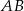AB wyliczymy z twierdzenia cosinusów w trójkącie 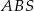ABS , a miarę kąta α z twierdzenia cosinusów w trójkącie ABC .

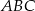Skoro dokładne wiemy, co będziemy robić, to do dzieła.

Piszemy twierdzenie cosinusów w trójkącie 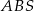ABS .

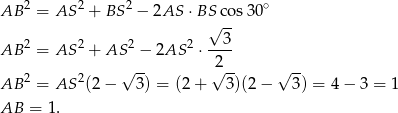
2 2 2 ∘ AB = AS + BS − 2AS ⋅ BS√ cos30 3 AB 2 = AS 2 + AS 2 − 2AS 2 ⋅---- √ -- √2-- √ -- AB 2 = AS 2(2 − 3) = (2 + 3 )(2− 3) = 4− 3 = 1 AB = 1.

Dalszą część rozwiązania przeprowadzimy na dwa sposoby.

Sposób I

Piszemy teraz twierdzenie cosinusów w trójkącie 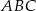ABC .

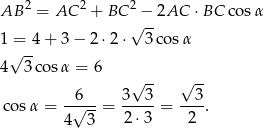
2 2 2 AB = AC + BC √−-2AC ⋅ BC cos α 1 = 4 + 3 − 2 ⋅2 ⋅ 3co sα √ -- 4 3 cosα = 6 √ -- √ -- co sα = -6√---= 3--3-= --3. 4 3 2⋅ 3 2

Zatem 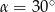α = 3 0∘ . Na mocy twierdzenia sinusów mamy

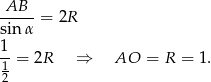
AB---= 2R sin α 1- 1 = 2R ⇒ AO = R = 1. 2

Możemy teraz wyliczyć długość wysokości ostrosłupa z trójkąta prostokątnego 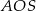AOS .

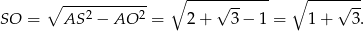
∘ ------------ ∘ ----√------- ∘ ----√--- SO = AS 2 − AO 2 = 2+ 3− 1 = 1 + 3.

Policzymy jeszcze pole podstawy – korzystamy ze wzoru z sinusem

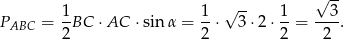
√ -- 1 1 √ -- 1 3 PABC = -BC ⋅AC ⋅sinα = --⋅ 3 ⋅2⋅ --= ---. 2 2 2 2

Zatem objętość ostrosłupa jest równa

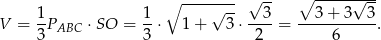
∘ ----√--- √ -- ∘ -----√--- V = 1P ⋅SO = 1⋅ 1+ 3⋅ --3-= --3-+-3--3-. 3 ABC 3 2 6

Sposób II

Jeżeli jesteśmy spostrzegawczy, to możemy zauważyć, że trójkąt 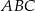ABC jest prostokątny

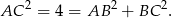
2 2 2 AC = 4 = AB + BC .

W takim razie punkt 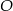O jest tak naprawdę środkiem odcinka 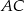AC (środek okręgu opisanego na trójkącie prostokątnym to środek przeciwprostokątnej) i mamy 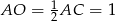AO = 1AC = 1 2 . Łatwo też możemy policzyć pole podstawy

√ -- 1- --3- PABC = 2AB ⋅BC = 2 .

Wysokość i objętość ostrosłupa liczymy jak poprzednio.  
Odpowiedź: √ 3+-3√3 V = ----6---

Wersja PDF