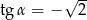Zadanie nr 2343339
Podstawą ostrosłupa 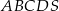 jest prostokąt
jest prostokąt 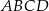 , w którym
, w którym 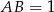 ,
, 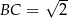 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
. Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz wartość dowolnej funkcji trygonometrycznej kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
Rozwiązanie
Zaczynamy oczywiście od rysunku.
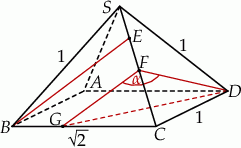
Zauważmy, że trójkąt  jest równoboczny, a trójkąt
jest równoboczny, a trójkąt  prostokątny (jest to połówka kwadratu). Najtrudniejsze w tym zadaniu to odpowiednio narysować płaszczyznę, w której będziemy liczyć miarę kąta między ścianami. Płaszczyzna ta musi być prostopadła do krawędzi kąta, w dodatku możemy tak ją wybrać, żeby przechodziła przez punkt
prostokątny (jest to połówka kwadratu). Najtrudniejsze w tym zadaniu to odpowiednio narysować płaszczyznę, w której będziemy liczyć miarę kąta między ścianami. Płaszczyzna ta musi być prostopadła do krawędzi kąta, w dodatku możemy tak ją wybrać, żeby przechodziła przez punkt 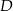 . W otrzymanym trójkącie
. W otrzymanym trójkącie 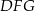 znamy długość boku
znamy długość boku 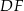 (wysokość w trójkącie równobocznym)
(wysokość w trójkącie równobocznym)
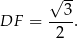
Aby wyliczyć pozostałe boki (liczymy je, żeby z twierdzenia cosinusów wyliczyć 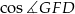 ) musimy ustalić, gdzie na boku
) musimy ustalić, gdzie na boku 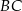 leży punkt
leży punkt 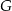 . To co wiemy, to że odcinek
. To co wiemy, to że odcinek 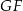 jest prostopadły do krawędzi
jest prostopadły do krawędzi 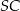 oraz
oraz 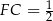 . Jak wcześniej zauważyliśmy,
. Jak wcześniej zauważyliśmy, 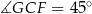 (bo
(bo 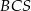 jest równoramiennym trójkątem prostokątnym). Zatem
jest równoramiennym trójkątem prostokątnym). Zatem 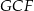 jest równoramiennym trójkątem prostokątnym, czyli
jest równoramiennym trójkątem prostokątnym, czyli
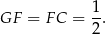
Ponadto 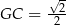 , więc z trójkąta prostokątnego
, więc z trójkąta prostokątnego 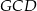 mamy
mamy
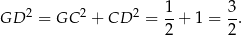
Stosujemy teraz twierdzenie cosinusów w trójkącie 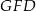 .
.
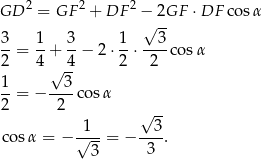
Stąd
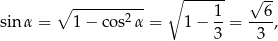
oraz
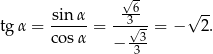
Odpowiedź: 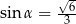 ,
, 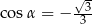 ,
,