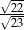Zadanie nr 3265689
Podstawą ostrosłupa 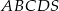 jest romb
jest romb 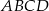 o boku długości 4. Kąt
o boku długości 4. Kąt 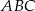 rombu ma miarę
rombu ma miarę 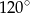 oraz
oraz 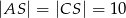 i
i 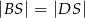 . Oblicz sinus kąta nachylenia krawędzi
. Oblicz sinus kąta nachylenia krawędzi 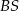 do płaszczyzny podstawy ostrosłupa.
do płaszczyzny podstawy ostrosłupa.
Rozwiązanie
Rozpoczynamy od rysunku.
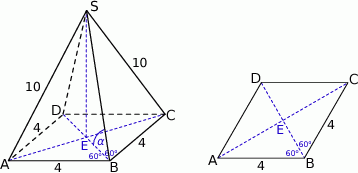
Zauważmy, że z równości 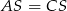 i
i 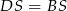 wynika, że spodek wysokości ostrosłupa pokrywa się z punktem wspólnym przekątnych rombu w podstawie. Interesujący nas kąt nachylenia krawędzi
wynika, że spodek wysokości ostrosłupa pokrywa się z punktem wspólnym przekątnych rombu w podstawie. Interesujący nas kąt nachylenia krawędzi 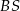 do płaszczyzny podstawy jest więc kątem
do płaszczyzny podstawy jest więc kątem 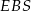 .
.
Ponieważ przekątne rombu są dwusiecznymi jego kątów wewnętrznych, wszystkie kąty trójkątów 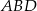 i
i 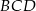 są równe
są równe 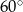 , czyli są to trójkąty równoboczne. W takim razie
, czyli są to trójkąty równoboczne. W takim razie
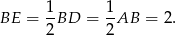
Ponadto, odcinek 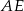 jest wysokością w trójkącie równobocznym o boku 4, więc
jest wysokością w trójkącie równobocznym o boku 4, więc
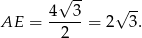
Korzystając z twierdzenia Pitagorasa w trójkącie 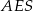 otrzymujemy
otrzymujemy
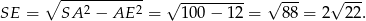
Stosujemy teraz twierdzenie Pitagorasa w trójkącie 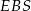 .
.
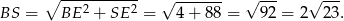
Pozostało obliczyć 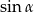 .
.
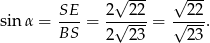
Odpowiedź: