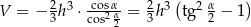Zadanie nr 3376502
W ostrosłupie prawidłowym czworokątnym 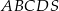 o podstawie
o podstawie 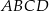 wysokość jest równa
wysokość jest równa 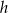 , a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Aby zaznaczyć kąt między dwoma sąsiednimi ścianami bocznymi ostrosłupa dorysowujemy dwie wysokości 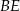 i
i 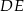 sąsiednich ścian bocznych.
sąsiednich ścian bocznych.
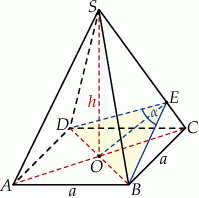
Płaszczyzna 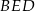 jest prostopadła do prostej
jest prostopadła do prostej 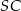 (bo zawiera dwie nierównoległe proste prostopadłe do
(bo zawiera dwie nierównoległe proste prostopadłe do 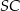 ), więc kąt
), więc kąt 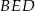 jest kątem między sąsiednimi ścianami bocznymi ostrosłupa.
jest kątem między sąsiednimi ścianami bocznymi ostrosłupa.
Jeżeli oznaczymy długość krawędzi podstawy przez  , to mamy
, to mamy
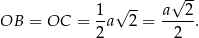
Sposób I
Z trójkąta prostokątnego 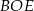 obliczamy długość odcinka
obliczamy długość odcinka 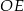 .
.
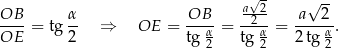
Korzystamy teraz z twierdzenia Pitagorasa w trójkącie prostokątnym 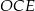 .
.
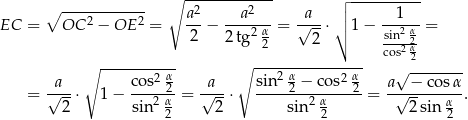
Zauważmy teraz, że trójkąty 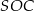 i
i 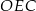 są oba prostokątne i mają wspólny kąt przy wierzchołku
są oba prostokątne i mają wspólny kąt przy wierzchołku 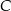 . Są więc podobne i mamy
. Są więc podobne i mamy
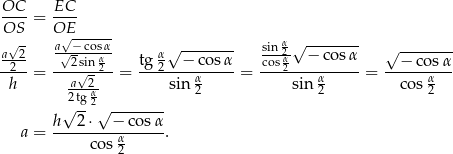
Pozostało jeszcze obliczyć objętość ostrosłupa
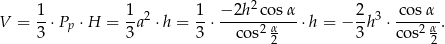
Sposób II
Stosujemy twierdzenie Pitagorasa w trójkącie prostokątnym  .
.
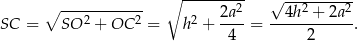
Obliczamy teraz długość odcinka 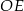 – można to zrobić porównując dwa wzory na pole trójkąta prostokątnego
– można to zrobić porównując dwa wzory na pole trójkąta prostokątnego 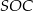 (
(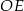 jest wysokością tego trójkąta), ale my zrobimy to inaczej – korzystamy z podobieństwa trójkątów prostokątnych
jest wysokością tego trójkąta), ale my zrobimy to inaczej – korzystamy z podobieństwa trójkątów prostokątnych 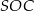 i
i 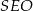 .
.
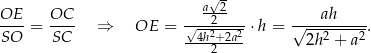
Teraz patrzymy na trójkąt prostokątny 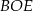 . Mamy w nim
. Mamy w nim
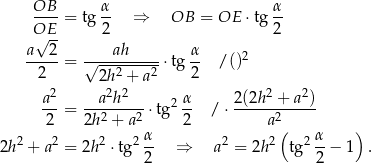
Pozostało jeszcze obliczyć objętość ostrosłupa
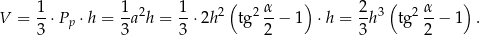
Odpowiedź: