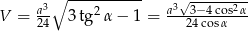/Szkoła średnia/Geometria/Stereometria/Ostrosłup

Zadanie nr 4002720

Dodaj do ulubionych
Dodaj do rozwiązanych

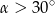W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość a . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę α > 30∘ . Oblicz objętość ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku.

PIC

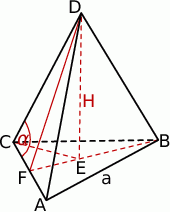
Ponieważ znamy długość krawędzi podstawy, wystarczy obliczyć wysokość 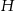H ostrosłupa. Zauważmy najpierw, że

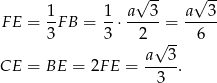
√ -- √ -- 1- 1- a---3 a---3 F E = 3FB = 3 ⋅ 2 = 6 √ -- CE = BE = 2F E = a--3. 3

Sposób I

Najpierw z trójkąta 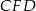CF D obliczamy wysokość ściany bocznej ostrosłupa.

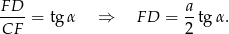
F D a ---- = tg α ⇒ FD = -tg α. CF 2

Teraz korzystamy z twierdzenia Pitagorasa w trójkącie 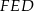FED .

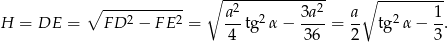
∘ -------------- ∘ ---------- ∘ ----------- a2 3a 2 a 1 H = DE = F D 2 − FE2 = ---tg2α − ----= -- tg2α − -. 4 36 2 3

Objętość ostrosłupa jest więc równa

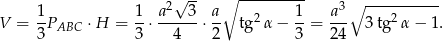
√ -- ∘ ---------- ∘ ----------- 1- 1- a-2--3 a- 2 1- a3- 2 V = 3PABC ⋅H = 3 ⋅ 4 ⋅ 2 tg α− 3 = 24 3tg α− 1.

Sposób II

Tym razem obliczymy najpierw długość krawędzi bocznej ostrosłupa.

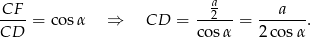
CF a2 a ----= cosα ⇒ CD = -----= -------. CD cosα 2 cosα

Teraz korzystamy z twierdzenia Pitagorasa w trójkącie 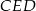CED .

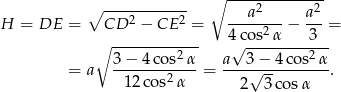
∘ -------------- ∘ ------------ a 2 a 2 H = DE = CD 2 − CE 2 = -----2--− ---= ∘ ------------ 4√co-s-α----3-- 3 − 4 cos2α a 3 − 4 cos2α = a -1-2cos2-α--= ----√----------. 2 3cos α

Objętość ostrosłupa jest więc równa

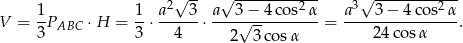
2√ -- √ --------2--- 3√ --------2--- V = 1-PABC ⋅H = 1-⋅ a--3-⋅ a--3√−-4-cos--α = a----3−--4cos--α. 3 3 4 2 3 cosα 2 4cos α

 
Odpowiedź: a3∘ ----------- a3√3−4-cos2α V = 24 3tg2α − 1 = ---24cosα---

Wersja PDF