Zadanie nr 6975521
W ostrosłupie, którego podstawą jest trójkąt równoboczny o boku  , jedna z krawędzi bocznych jest prostopadła do podstawy. Dwie pozostałe krawędzie tworzą z podstawą kąty o mierze
, jedna z krawędzi bocznych jest prostopadła do podstawy. Dwie pozostałe krawędzie tworzą z podstawą kąty o mierze  . Znajdź pole największej ściany bocznej oraz tangens kąta nachylenia tej ściany do płaszczyzny podstawy.
. Znajdź pole największej ściany bocznej oraz tangens kąta nachylenia tej ściany do płaszczyzny podstawy.
Rozwiązanie
Zaczynamy od rysunku.
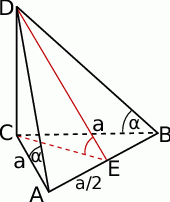
Zaczniemy od wyliczenia wysokości 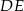 trójkąta
trójkąta 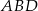 . Z trójkąta
. Z trójkąta 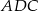 wyliczamy długość odcinka
wyliczamy długość odcinka 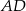 .
.
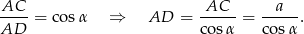
Teraz z trójkąta prostokątnego 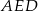 wyliczamy
wyliczamy 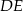 .
.
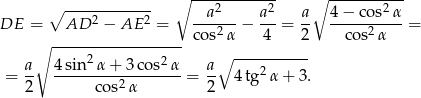
Zatem pole trójkąta 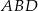 jest równe
jest równe
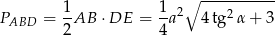
Mamy
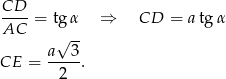
Zatem
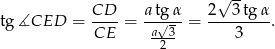
Odpowiedź: Pole: 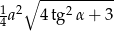 , tangens:
, tangens: