/Szkoła średnia/Geometria/Stereometria/Ostrosłup

Zadanie nr 7336033

Dodaj do ulubionych
Dodaj do rozwiązanych

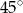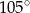Podstawą ostrosłupa jest trójkąt, którego jeden z boków ma długość 6, a kąty przyległe do niego mają miary 45∘ i 105∘ . Wysokość ostrosłupa ma długość równą długości promienia okręgu opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci 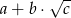a+ b⋅√c- , gdzie 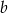a , b , c są liczbami wymiernymi.

Rozwiązanie

Po pierwsze, zadanie w ogóle nie jest przestrzenne. Aby obliczyć objętość, potrzebujemy pole podstawy i wysokość, a skoro wysokość jest równa promieniowi okręgu opisanego na podstawie, to cała akcja dzieje się w trójkącie podstawy.

PIC

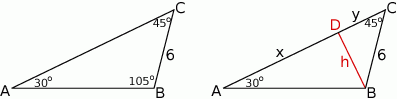
Ponieważ trzeci kąt trójkąta ma miarę 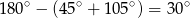18 0∘ − (45∘ + 105∘) = 30 ∘ , to z twierdzenia sinusów wyliczamy promień okręgu opisanego R .

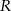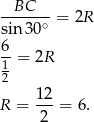
-BC----= 2R sin 30∘ 6 1-= 2R 2 1-2 R = 2 = 6.

Sposób I

Wyliczamy długość boku 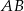AB .

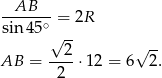
--AB--- = 2R sin4 5∘√ -- 2 √ -- AB = ---⋅ 12 = 6 2. 2

Teraz obliczymy 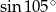sin 105∘ (żeby móc policzyć pole ze wzoru z sinusem).

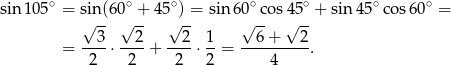
sin1 05∘ = sin(60∘ + 45∘) = sin 60∘ cos45 ∘ + sin 45∘co s60∘ = √ -- √ -- √ -- √ -- √ -- --3- --2- --2- 1- --6-+---2- = 2 ⋅ 2 + 2 ⋅2 = 4 .

Obliczamy pole podstawy

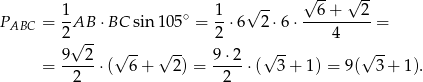
√ -- √ -- √ -- PABC = 1-AB ⋅BC sin 105∘ = 1-⋅6 2⋅6 ⋅--6-+---2-= 2 √ -- 2 4 9 2 √ -- √ -- 9 ⋅2 √ -- √ -- = -----⋅ ( 6+ 2) = ---- ⋅( 3+ 1) = 9( 3 + 1). 2 2

No i liczymy objętość

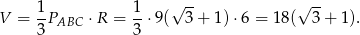
1- 1- √ -- √ -- V = 3 PABC ⋅ R = 3 ⋅ 9( 3+ 1)⋅6 = 18( 3 + 1).

Sposób II

Pole trójkąta 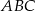ABC można też wyliczyć inaczej.

Jeżeli poprowadzimy wysokość 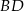BD z wierzchołka 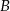B , to trójkąt 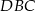DBC jest połówką kwadratu, więc 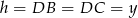h = DB = DC = y oraz

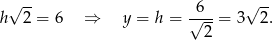
√ -- √ -- h 2 = 6 ⇒ y = h = √6--= 3 2. 2

Patrzymy teraz na trójkąt prostokątny 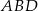ABD .

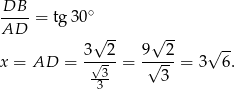
DB ---- = tg 30∘ AD √ -- √ -- 3---2 9---2 √ -- x = AD = √-3 = √ 3- = 3 6. 3

Mamy zatem 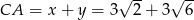√ -- √ -- CA = x + y = 3 2 + 3 6 i pole trójkąta 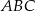ABC jest równe

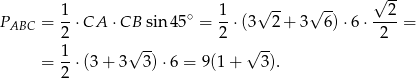
√ -- √ -- √ -- P = 1-⋅CA ⋅CB sin 45∘ = 1⋅(3 2+ 3 6)⋅6 ⋅---2 = ABC 2 2 2 1 √ -- √ -- = 2-⋅(3 + 3 3) ⋅6 = 9(1 + 3).

Objętość ostrosłupa jest więc równa

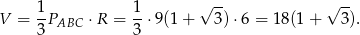
1- 1- √ -- √ -- V = 3 PABC ⋅ R = 3 ⋅ 9(1+ 3)⋅6 = 18(1 + 3).

 
Odpowiedź: √ -- 18 + 18 3

Wersja PDF