/Szkoła średnia/Geometria/Stereometria/Ostrosłup

Zadanie nr 8774194

Dodaj do ulubionych
Dodaj do rozwiązanych

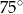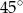Podstawą ostrosłupa jest trójkąt, którego jeden bok ma długość 4, a kąty przyległe do tego boku mają miary 75 ∘ i 45∘ . Wysokość ostrosłupa ma długość równą długości promienia koła opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci 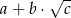a+ b⋅√c , gdzie a , b , c są liczbami wymiernymi.

Rozwiązanie

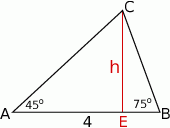
Po pierwsze, zadanie w ogóle nie jest przestrzenne. Aby obliczyć objętość, potrzebujemy pole podstawy i wysokość, a skoro wysokość jest równa promieniowi okręgu opisanego na podstawie, to cała akcja dzieje się w trójkącie podstawy.

PIC

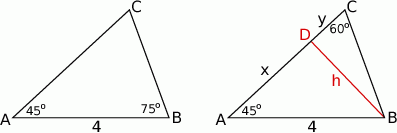
Ponieważ trzeci kąt trójkąta ma miarę 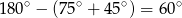1 80∘ − (75∘ + 45∘) = 60 ∘ , to z twierdzenia sinusów wyliczamy promień okręgu opisanego R .

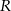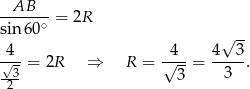
--AB--- = 2R sin60 ∘ -- 4 4 4√ 3 √-- = 2R ⇒ R = √---= -----. -23 3 3

Podobnie wyliczamy długość boku 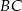BC .

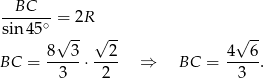
--BC--- sin4 5∘ = 2R √ -- √ -- √ -- BC = 8---3⋅ --2- ⇒ BC = 4--6. 3 2 3

Pokażemy teraz trzy sposoby dokończenia rozwiązania zadania.

Sposób I

Obliczymy 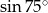sin75 ∘ (żeby móc policzyć pole ze wzoru z sinusem).

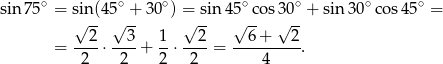
∘ ∘ ∘ ∘ ∘ ∘ ∘ sin 75 = si√n(4 5√ +- 30 ) =√ sin45√-cos√30-+ sin 30 cos4 5 = 2 3 1 2 6 + 2 = ----⋅----+ --⋅ ----= ----------. 2 2 2 2 4

Liczymy najpierw pole podstawy

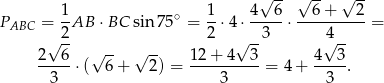
√ -- √ -- √ -- PABC = 1-AB ⋅BC sin75 ∘ = 1-⋅4 ⋅ 4-6-⋅--6-+---2-= √ 2- 2 √ --3 4√ -- 2 6 √ -- √ -- 12+ 4 3 4 3 -----⋅( 6 + 2) = ----------= 4 + ----. 3 3 3

No i liczymy objętość

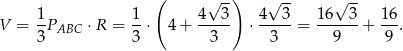
( ) 1 1 4√ 3- 4√ 3- 16√ 3- 16 V = -PABC ⋅ R = -⋅ 4 + ----- ⋅ -----= ------+ --. 3 3 3 3 9 9

Sposób II

Dorysujmy wysokość 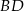BD opuszczoną z wierzchołka 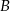B . Trójkąt 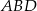ABD jest połówką kwadratu, więc

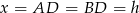
x = AD = BD = h

oraz

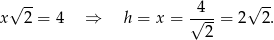
√ -- 4 √ -- x 2 = 4 ⇒ h = x = √---= 2 2. 2

Patrzymy teraz na trójkąt prostokątny 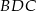BDC .

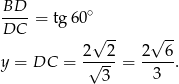
BD ----= tg60 ∘ DC √ -- √ -- 2--2- 2--6- y = DC = √ --= 3 . 3

Stąd 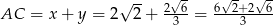√ - √ - √- √ -- 2--6 6--2+-2-6 AC = x+ y = 2 2 + 3 = 3 i pole trójkąta 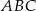ABC jest równe

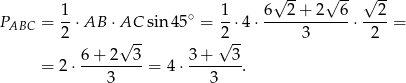
√ -- √ -- √ -- PABC = 1⋅ AB ⋅ AC sin 45∘ = 1-⋅4 ⋅ 6--2+-2---6⋅ --2-= 2 √ -- 2√ -- 3 2 6 + 2 3 3 + 3 = 2 ⋅---------= 4 ⋅-------. 3 3

Objętość obliczamy tak, jak w poprzednim sposobie.

Sposób III

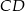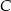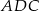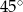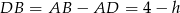Jeżeli poprowadzimy wysokość CD z wierzchołka C , to trójkąt ADC jest równoramienny (bo ma dwa kąty równe 45∘ ), zatem DB = AB − AD = 4 − h .

PIC

Stosujemy teraz twierdzenie Pitagorasa w trójkącie 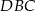DBC .

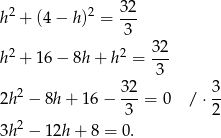
2 2 32 h + (4− h) = --- 3 h2 + 16− 8h + h2 = 32- 3 2 3-2 3- 2h − 8h + 16 − 3 = 0 / ⋅ 2 2 3h − 12h + 8 = 0.

Dalej, 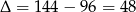Δ = 144 − 96 = 48 ,

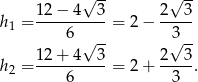
√ -- √ -- h = 1-2−-4---3 = 2 − 2---3 1 6 √ -- 3√ -- 1 2+ 4 3 2 3 h 2 =---------- = 2 + -----. 6 3

Ponieważ odcinek 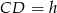CD = h leży naprzeciwko kąta o mierze 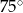∘ 75 w trójkącie prostokątnym, to 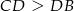CD > DB , co wyklucza pierwsze rozwiązanie. Zatem 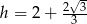√- h = 2+ 2-3- 3 oraz

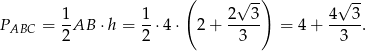
( √ --) √ -- 1- 1- 2--3- 4--3- PABC = 2 AB ⋅h = 2 ⋅4 ⋅ 2 + 3 = 4+ 3 .

Objętość obliczamy tak, jak w poprzednich sposobach.  
Odpowiedź: √ -- 169 + 169 3

Wersja PDF