Zadanie nr 9228274
Podstawą ostrosłupa 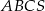 jest trójkąt
jest trójkąt 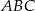 o bokach długości 18 cm i 12 cm, którego kąt między tymi bokami ma miarę równą
o bokach długości 18 cm i 12 cm, którego kąt między tymi bokami ma miarę równą 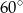 . Wszystkie krawędzie boczne ostrosłupa
. Wszystkie krawędzie boczne ostrosłupa 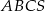 mają długości równe 12 cm. Ostrosłup ten przecięto płaszczyzną równoległą do podstawy i dzielącą jego wysokość w stosunku 1:2, licząc od wierzchołka tego ostrosłupa. Wykonaj rysunek ostrosłupa
mają długości równe 12 cm. Ostrosłup ten przecięto płaszczyzną równoległą do podstawy i dzielącą jego wysokość w stosunku 1:2, licząc od wierzchołka tego ostrosłupa. Wykonaj rysunek ostrosłupa 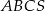 z zaznaczonym przekrojem i oblicz:
z zaznaczonym przekrojem i oblicz:
- obwód otrzymanego przekroju,
- objętość tej z brył wyznaczonych przez przekrój, która nie jest podobna do ostrosłupa
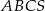 .
.
Rozwiązanie
Zaczynamy oczywiście od rysunku.
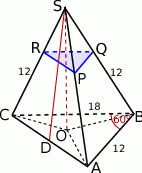
- Zauważmy, że otrzymany ostrosłup
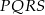 jest podobny do ostrosłupa
jest podobny do ostrosłupa 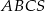 w skali
w skali 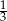 . Zatem obwód trójkąta
. Zatem obwód trójkąta 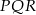 jest równy
jest równy 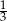 obwodu trójkąt
obwodu trójkąt 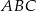 . Aby wyliczyć obwód trójkąta
. Aby wyliczyć obwód trójkąta 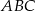 , musimy wyliczyć długość boku
, musimy wyliczyć długość boku 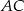 – możemy to łatwo zrobić z twierdzenia cosinusów.
– możemy to łatwo zrobić z twierdzenia cosinusów. 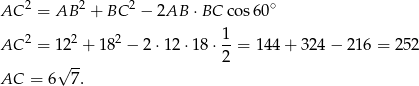
Zatem obwód trójkąta
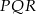 jest równy
jest równy 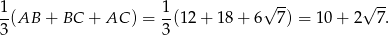
Odpowiedź: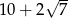
- Plan jest następujący: objętość interesującej nas bryły to różnica objętości dużego i małego ostrosłupa. Z podobieństwa tych ostrosłupów, ta różnica objętości jest równa
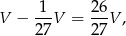
gdzie przez
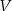 oznaczyliśmy objętość ostrosłupa
oznaczyliśmy objętość ostrosłupa 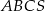 . Do wyliczenia
. Do wyliczenia 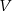 brakuje nam wysokości ostrosłupa. Ponieważ wszystkie krawędzie boczne są równe, spodek wysokości
brakuje nam wysokości ostrosłupa. Ponieważ wszystkie krawędzie boczne są równe, spodek wysokości 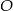 ostrosłupa to dokładnie środek okręgu opisanego na trójkącie
ostrosłupa to dokładnie środek okręgu opisanego na trójkącie 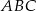 (bo trójkąty
(bo trójkąty 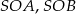 i
i 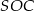 są przystające). Zatem do wyliczenia wysokości potrzebna nam jest długość promienia okręgu opisanego na trójkącie
są przystające). Zatem do wyliczenia wysokości potrzebna nam jest długość promienia okręgu opisanego na trójkącie 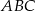 . Tę jednak możemy łatwo wyliczyć z twierdzenia sinusów.
. Tę jednak możemy łatwo wyliczyć z twierdzenia sinusów. 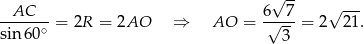
Stosujemy teraz twierdzenie Pitagorasa w trójkącie
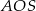 .
. 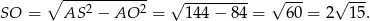
Wyliczmy jeszcze pole podstawy ostrosłupa.
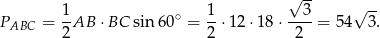
Zatem interesująca nas objętość jest równa
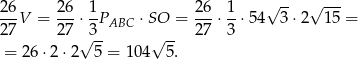
Odpowiedź: