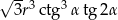Zadanie nr 9359023
W ostrosłup prawidłowy trójkątny wpisano kulę o promieniu  . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem
. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 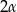 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Zaczynamy od rysunku.
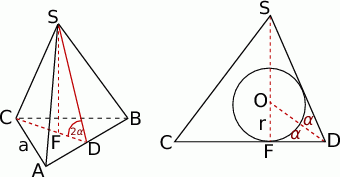
Co wiemy o środku kuli wpisanej w ten czworościan? – na pewno leży on na wysokości 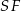 , oraz na dwusiecznej
, oraz na dwusiecznej 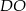 kąta
kąta 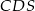 . To pozwala łatwo wyliczyć krawędź
. To pozwala łatwo wyliczyć krawędź  podstawy ostrosłupa. Zauważmy, że odcinek
podstawy ostrosłupa. Zauważmy, że odcinek 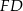 stanowi
stanowi 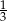 wysokości trójkąta równobocznego w podstawie. Patrząc na trójkąt
wysokości trójkąta równobocznego w podstawie. Patrząc na trójkąt 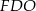 mamy
mamy
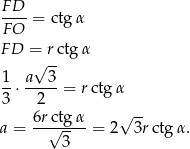
Z trójkąta 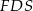 wyliczamy wysokość
wyliczamy wysokość 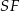 .
.
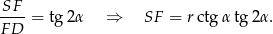
Teraz możemy policzyć objętość ostrosłupa (korzystamy ze wzoru na pole trójkąta równobocznego).
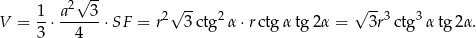
Odpowiedź: