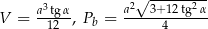/Szkoła średnia/Geometria/Stereometria/Ostrosłup

Zadanie nr 9638645

Dodaj do ulubionych
Dodaj do rozwiązanych

Ostrosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź podstawy długości a i środek wysokości ostrosłupa. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem α . Oblicz objętość i pole powierzchni bocznej ostrosłupa.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

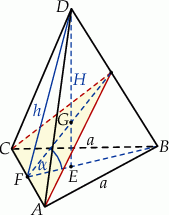
Ustalmy najpierw plan działania. Ponieważ znamy długość krawędzi podstawy, do obliczenia objętości brakuje nam wysokości 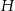H . Wiemy, że 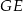GE jest połową wysokości i długość tego odcinka będziemy mogli obliczyć z trójkąta 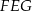F EG . Gdy już będziemy mieli wysokość, z trójkąta 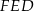FED wyliczymy wysokość ściany bocznej, co pozwoli obliczyć pole powierzchni bocznej.

Wiemy już co mamy robić, więc do dzieła. Ponieważ 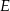E jest środkiem trójkąta równobocznego w podstawie, odcinek 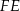FE stanowi 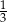1 3 długości wysokości tego trójkąta. Zatem

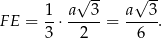
1 a√ 3- a√ 3- FE = --⋅-----= -----. 3 2 6

Teraz patrzymy na trójkąt prostokątny 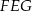F EG .

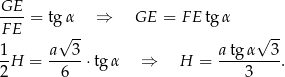
GE ---- = tg α ⇒ GE = F E tg α FE √ -- √ -- 1- a--3- atgα---3- 2 H = 6 ⋅tg α ⇒ H = 3 .

Możemy już obliczyć objętość ostrosłupa.

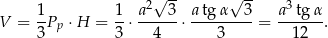
√ -- √ -- 1- 1- a-2--3 atg-α--3- a3tg-α- V = 3Pp ⋅H = 3 ⋅ 4 ⋅ 3 = 12 .

Patrzymy teraz na trójkąt prostokątny 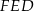FED .

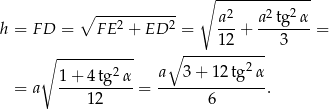
∘ -------------- ∘ ----------- a2 a2tg2 α h = FD = FE2 + ED 2 = ---+ --------= ∘ ----------- ∘ ----12------ 3 2 a 3+ 1 2tg2α = a 1-+-4-tg-α-= ---------------. 12 6

Liczymy teraz pole powierzchni bocznej.

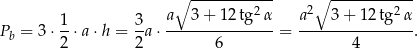
∘ ------------ ∘ ------------ a 3+ 1 2tg2α a 2 3+ 12tg2 α P = 3 ⋅ 1-⋅a ⋅h = 3a ⋅--------------- = ----------------. b 2 2 6 4

 
Odpowiedź: √ -------- V = a3tgα, P = a2--3+12tg2α 12 b 4

Wersja PDF