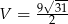/Szkoła średnia/Geometria/Stereometria/Ostrosłup

Zadanie nr 9722143

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa 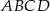ABCD jest trójkąt równoramienny 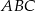ABC , w którym 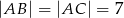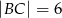|AB | = |AC | = 7 , |BC | = 6 . Krawędzie boczne mają długości: 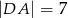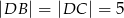|DA | = 7 , |DB | = |DC | = 5 . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Rozpoczynamy oczywiście od rysunku.

PIC

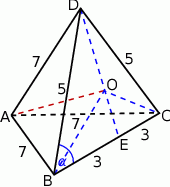
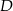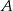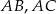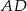Problemem w tym zadaniu jest to, że nie wiadomo gdzie jest spodek wysokości opuszczonej z wierzchołka D i to skutecznie utrudnia obliczenie długości tej wysokości. Zauważmy jednak, że o wiele lepiej jest z wysokością opuszczoną z wierzchołka A . Ponieważ krawędzie AB ,AC i AD mają równą długość, trójkąty prostokątne 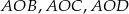AOB ,AOC ,AOD są przystające, czyli 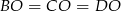BO = CO = DO , co oznacza, że spodek wysokości 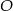O jest środkiem okręgu opisanego na trójkącie 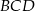BCD . W takim razie do obliczenia długości wysokości 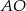AO ostrosłupa brakuje nam długości 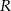R promienia okręgu opisanego na trójkącie 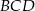BCD (bo wtedy zastosujemy twierdzenie Pitagorasa do trójkąta 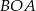BOA ). Długość promienia okręgu opisanego będziemy mogli wyliczyć z twierdzenia sinusów, jeżeli będziemy znali sinus jednego z kątów trójkąta 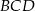BCD , np. 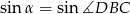sin α = sin ∡DBC .

Rozwiązanie sprowadziliśmy więc do obliczenia 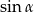sinα – aby to zrobić obliczamy najpierw długość wysokości 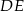DE w trójkącie równoramiennym DBC .

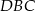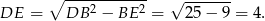
∘ ------------ √ ------- DE = DB 2 − BE 2 = 25 − 9 = 4 .

Mamy zatem

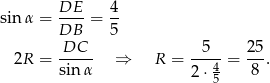
DE 4 sin α = ----= -- DB 5 DC--- -5--- 25- 2R = sin α ⇒ R = 2⋅ 4 = 8 . 5

Korzystamy teraz z twierdzenia Pitagorasa w trójkącie 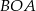BOA

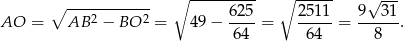
∘ ------------ ∘ --------- ∘ ------ √ --- AO = AB 2 − BO 2 = 49 − 625-= 2511-= 9--3-1. 64 64 8

Pozostało obliczyć objętość ostrosłupa.

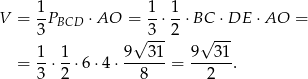
1 1 1 V = -PBCD ⋅AO = --⋅--⋅BC ⋅DE ⋅AO = 3 √ 3--2 √ --- 1 1 9 31 9 31 = --⋅--⋅6 ⋅4 ⋅------= ------. 3 2 8 2

 
Odpowiedź: √ -- 9--31 V = 2

Wersja PDF