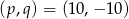Zadanie nr 1984880
Wielomiany 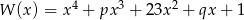 oraz
oraz 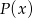 są wielomianami o współczynnikach całkowitych, przy czym
są wielomianami o współczynnikach całkowitych, przy czym ![W (x ) = [P (x)]2](https://img.zadania.info/zad/1984880/HzadT2x.gif) . Wyznacz wszystkie możliwe wartości
. Wyznacz wszystkie możliwe wartości 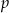 i
i 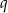 .
.
Rozwiązanie
Z równości
![4 3 2 2 W (x ) = x + px + 23x + qx + 1 = [P(x)]](https://img.zadania.info/zad/1984880/HzadR0x.gif)
wynika, że 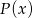 musi być wielomianem stopnia 2, czyli musi mieć postać
musi być wielomianem stopnia 2, czyli musi mieć postać
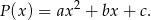
Żeby trochę zmniejszyć liczbę możliwości, zauważmy jeszcze, że możemy założyć, że 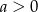 . Tak jest, bo jeżeli
. Tak jest, bo jeżeli ![W (x ) = [P(x)]2](https://img.zadania.info/zad/1984880/HzadR4x.gif) to też
to też ![W (x) = [−P (x)]2](https://img.zadania.info/zad/1984880/HzadR5x.gif) . Mamy zatem
. Mamy zatem
![2 2 2 2 4 2 2 2 3 2 [P (x)] = (ax + bx + c) = a x + b x + c + 2abx + 2acx + 2bcx = = a2x4 + 2abx3 + (b2 + 2ac)x2 + 2bcx + c2.](https://img.zadania.info/zad/1984880/HzadR6x.gif)
Stąd
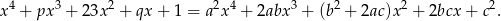
Jeżeli popatrzymy na współczynnik przy 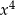 i na wyraz wolny to widzimy, że
i na wyraz wolny to widzimy, że 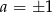 i
i 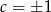 . Dzięki naszemu założeniu
. Dzięki naszemu założeniu 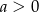 , mamy zatem
, mamy zatem 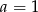 i
i
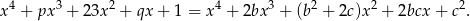
Jeżeli 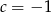 , to mamy równość
, to mamy równość
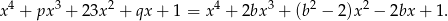
Porównując współczynniki przy 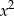 mamy
mamy 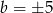 . Daje to nam dwa możliwe rozwiązania:
. Daje to nam dwa możliwe rozwiązania: 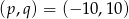 lub
lub 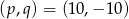 .
.
Jeżeli natomiast 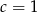 , to mamy równość
, to mamy równość
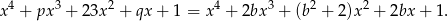
Taka sytuacja jest jednak niemożliwa, bo po porównaniu współczynników przy 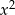 otrzymujemy
otrzymujemy 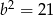 .
.
Odpowiedź: 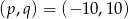 lub
lub