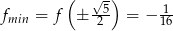Zadanie nr 3752024

Funkcja 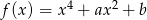4 2 f(x) = x + ax + b przyjmuje wartość 1 dla czterech argumentów:

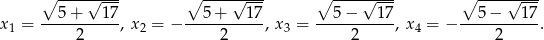
∘ ----√---- ∘ ----√---- ∘ ----√---- ∘ ----√---- x = ---5+----17, x = − --5-+---1-7, x = --5-−---17-, x = − --5-−---17-. 1 2 2 2 3 2 4 2

Oblicz najmniejszą wartość tej funkcji.

Wersja PDF

Rozwiązanie

Mamy podane 4 miejsca zerowe funkcji

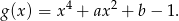
4 2 g(x) = x + ax + b− 1 .

Jeżeli podstawimy 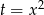2 t = x , to liczby

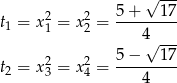
√ --- t = x2 = x2 = 5+----17- 1 1 2 4 --- 5− √ 17 t2 = x23 = x24 = --------- 4

są pierwiastkami równania

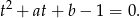
2 t + at+ b− 1 = 0.

Na mocy wzorów Viète’a to z kolei oznacza, że

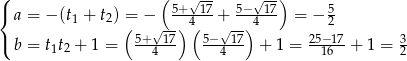
( { ( 5+-√17- 5−-√17) 5 a = − (t1 + t2) =( −√--) 4( +√ --)4 = − 2 ( b = t t + 1 = 5+--17- 5−--17 + 1 = 25−-17 + 1 = 3 1 2 4 4 16 2

Wykresem funkcji

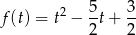
5 3 f(t) = t2 − -t+ -- 2 2

jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość przyjmuje dla

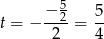
− 5 t = − --2-= 5- 2 4

i jest ona równa

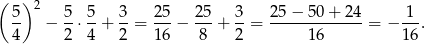
( ) 2 5- − 5-⋅ 5-+ 3-= 25-− 25-+ 3-= 25-−-50-+-24-= − -1-. 4 2 4 2 16 8 2 16 16

Wartość tę funkcja

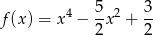
f(x) = x4 − 5-x2 + 3- 2 2

przyjmuje dla argumentu 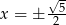√- x = ± -52- .

Na koniec wykres funkcji 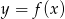y = f (x) dla ciekawskich.

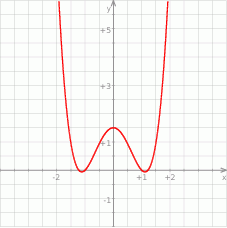
Odpowiedź: ( √-) fmin = f ± 25- = − 116