Zadanie nr 3697429
Trójkąty 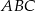 i
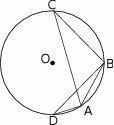
i 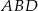 zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że
zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że 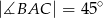 oraz
oraz 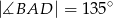 . Wówczas długości cięciw
. Wówczas długości cięciw 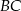 i
i 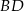 spełniają zależność
spełniają zależność
A) 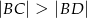
B) 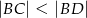
C) 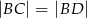
D) 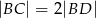
E) 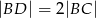
Rozwiązanie
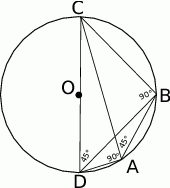
Z podanych kątów wynika, że 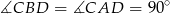 . Ponadto
. Ponadto 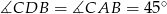 . Zatem trójkąt
. Zatem trójkąt 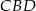 jest prostokątny i ma kąt ostry równy
jest prostokątny i ma kąt ostry równy 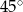 . W szczególności jest równoramienny.
. W szczególności jest równoramienny.
Odpowiedź: C

