/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Styczne do wykresu

Zadanie nr 1844163

Dodaj do ulubionych
Dodaj do rozwiązanych

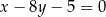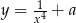Wyznacz wszystkie wartości parametru a , dla których prosta o równaniu x − 8y − 5 = 0 jest styczna do wykresu funkcji y = x14 + a .

Rozwiązanie

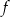Dana prosta ma współczynnik kierunkowy 1 8 – liczymy pochodną funkcji f i sprawdzamy w jakim punkcie przyjmuje taką wartość.

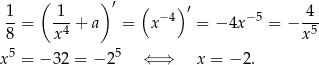
( )′ ( ) 1-= -1-+ a = x−4 ′ = −4x −5 = − 4-- 8 x 4 x5 5 5 x = − 32 = − 2 ⇐ ⇒ x = − 2 .

Dana prosta musi być więc styczna w punkcie o pierwszej współrzędnej równej 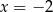x = − 2 . Druga współrzędna punktu styczności to

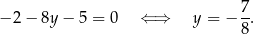
− 2 − 8y − 5 = 0 ⇐ ⇒ y = − 7. 8

Pozostało sprawdzić, dla jakiego a , wykres danej funkcji przechodzi przez punkt o współrzędnych ( ) − 2,− 78

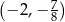
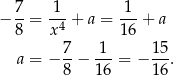
− 7-= 1--+ a = 1--+ a 8 x4 16 7 1 15 a = − 8-− 16-= − 16.

Na koniec obrazek dla ciekawskich.

PIC

 
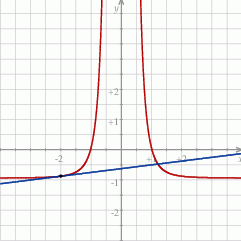
Odpowiedź: a = − 1516-

Wersja PDF