/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Styczne do wykresu

Zadanie nr 1859520

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie styczne do wykresu funkcji 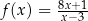8x+1- f(x) = x− 3 , które razem z osiami układu współrzędnych ograniczają trójkąt równoramienny.

Rozwiązanie

Zauważmy, że styczna i osie układu współrzędnych zawsze ograniczają trójkąt prostokątny. Jeżeli więc ten trójkąt ma być równoramienny, to jest to połówka kwadratu z kątem ostrym równym 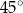45∘ . Nadal możliwe są dwie różne sytuacje – w zależności od tego, czy styczna ma dodatni czy ujemny współczynnik kierunkowy.

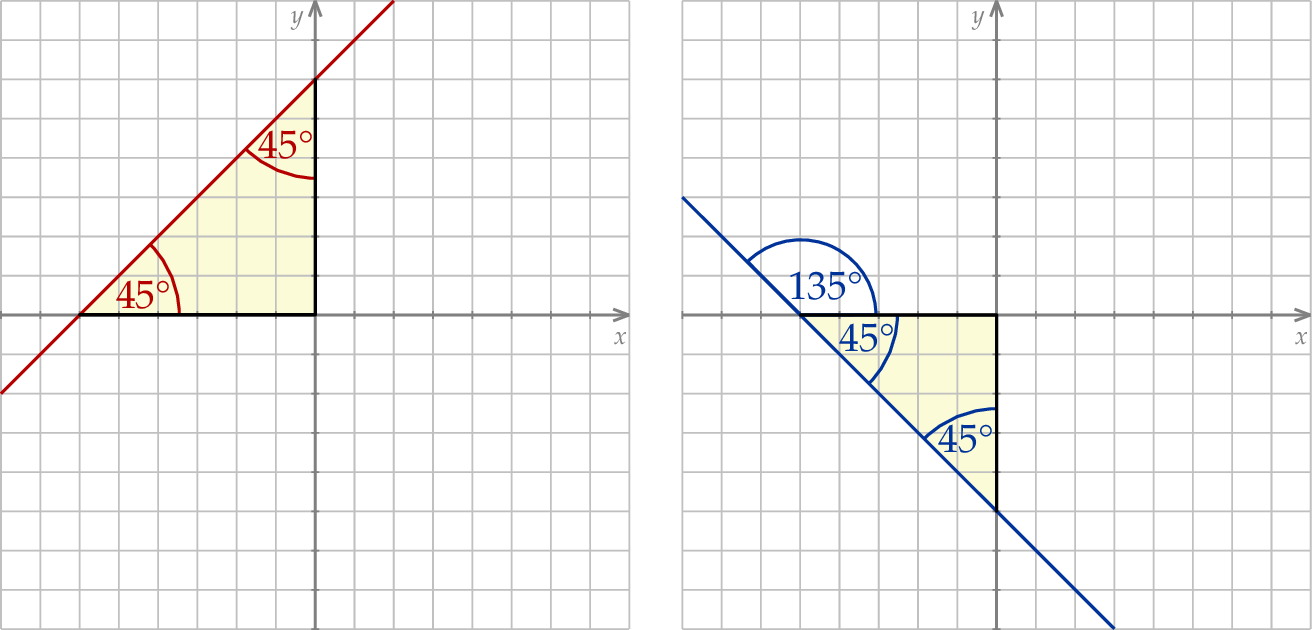
ZINFO-FIGURE

W pierwszym przypadku kąt nachylenia do osi 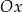Ox musi być równy 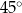4 5∘ , a w drugim 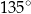1 35∘ . Tangensy tych kątów to odpowiednio 1 i 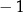− 1 . Będziemy korzystać z tego, że współczynnik kierunkowy stycznej do wykresu funkcji 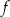f w punkcie 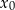x 0 jest równy pochodnej 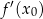′ f (x0) w tym punkcie. Liczymy pochodną

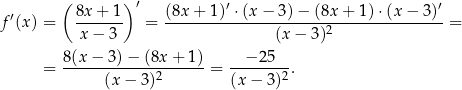
( ) ′ ′ ′ f′(x) = 8x-+--1 = (8x-+-1)-⋅(x-−-3-)−-(8x-+-1-)⋅(x-−-3)--= x − 3 (x − 3)2 = 8(x-−-3)−--(8x-+-1)-= --−-25--. (x − 3 )2 (x− 3)2

Widać, ze pochodna jest stale ujemna, więc nigdy nie jest równa 1. Sprawdźmy kiedy jest równa 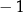− 1 .

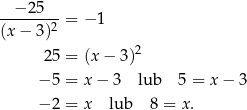
− 25 -------2-= −1 (x − 3) 25 = (x− 3)2 − 5 = x− 3 lub 5 = x − 3 − 2 = x lub 8 = x.

Obliczmy jeszcze wartość funkcji 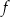f w tych dwóch punktach.

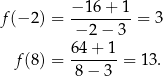
−-1-6+-1- f(− 2) = − 2 − 3 = 3 f(8) = 6-4+--1 = 13. 8 − 3

Są więc dwie styczne spełniające warunki zadania

y = − 1⋅(x + 2 )+ 3 = −x + 1 y = − 1⋅(x − 8 )+ 13 = −x + 21.

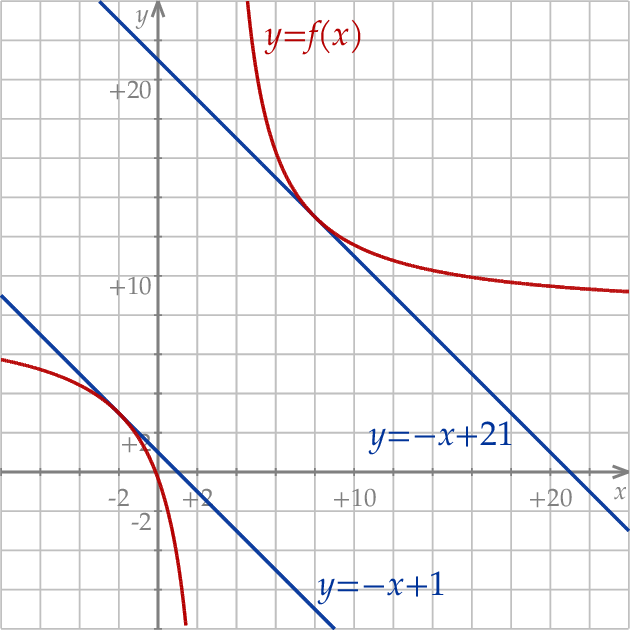
Na koniec obrazek dla ciekawskich.

ZINFO-FIGURE

 
Odpowiedź: 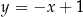y = −x + 1 i y = −x + 21

Wersja PDF