/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Styczne do wykresu

Zadanie nr 3532567

Dodaj do ulubionych
Dodaj do rozwiązanych

Napisz równanie stycznych do wykresu funkcji 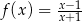x−1- f(x) = x+1 i równoległych do prostej o równaniu y = 2x + 1 .

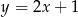Rozwiązanie

Sposób I

Musimy znaleźć punkty na hiperboli, w których styczna ma wpółczynnik kierunkowy 2. Idealnym do tego narzędziem jest pochodna. Pochodna w punkcie to dokładnie wpółczynnik kierunkowy stycznej w tym punkcie. Liczymy pochodną

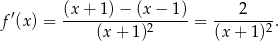
′ (x-+-1-)−-(x-−-1-) ----2---- f (x) = (x + 1)2 = (x + 1)2 .

Sprawdzamy kiedy pochodna równa się 2.

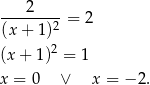
2 (x-+-1)2-= 2 (x+ 1)2 = 1 x = 0 ∨ x = − 2.

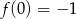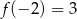Ponieważ f (0) = − 1 i f(− 2) = 3 , to szukane styczne to proste postaci 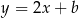y = 2x+ b przechodzące przez te punkty. Bez trudu wyliczamy, że 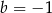b = − 1 lub b = 7 .

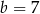Sposób II

Ponieważ

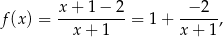
f(x) = x+--1−--2-= 1 + -−-2--, x+ 1 x + 1

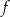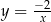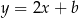to wykres funkcji f jest hiperbolą y = −x2- przesuniętą o wektor [− 1,1 ] . W szczególności prosta postaci y = 2x + b jest styczna do hiperboli tylko wtedy gdy ma z nią dokładnie jeden punkt wspólny (bo nie jest równoległa do asymptot! - to jest ważne). Liczymy

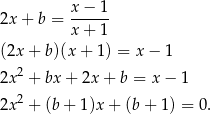
x − 1 2x + b = ------ x + 1 (2x + b)(x+ 1) = x − 1 2x 2 + bx+ 2x + b = x − 1 2x 2 + (b+ 1 )x+ (b+ 1) = 0.

Musimy sprawdzić, kiedy to równanie ma dokładnie jedno rozwiązanie, czyli kiedy 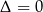Δ = 0 . Liczymy

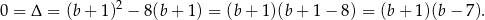
2 0 = Δ = (b+ 1 ) − 8(b + 1 ) = (b+ 1)(b+ 1− 8) = (b+ 1)(b− 7).

Zatem 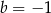b = − 1 lub b = 7 .

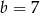Na koniec, dla ciekawskich, wykres całej sytuacji.

PIC

 
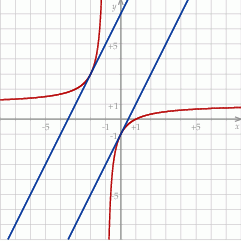
Odpowiedź: 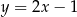y = 2x− 1 i y = 2x + 7

Wersja PDF