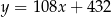/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Styczne do wykresu

Zadanie nr 7311133

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równanie stycznej do wykresu funkcji 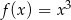3 f(x) = x , która przecina oś Ox w jednym punkcie: (− 4,0) .

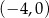Rozwiązanie

Wyznaczmy najpierw równanie stycznej do wykresu funkcji 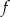f w punkcie 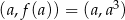(a,f (a)) = (a,a3) . Liczymy pochodną.

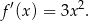
f′(x) = 3x 2.

Współczynnik kierunkowy stycznej do wykresu w punkcie 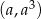(a,a3) jest więc równy 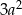3a2 i styczna ta ma postać 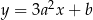y = 3a2x + b . Współczynnik 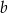b wyznaczamy podstawiając współrzędne punktu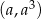 (a,a3)

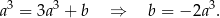
3 3 3 a = 3a + b ⇒ b = −2a .

Styczna ma więc równanie 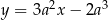y = 3a2x − 2a3 . Wyznaczamy teraz punkt wspólny tej stycznej z osią Ox .

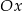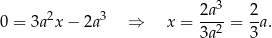
2a3 2 0 = 3a2x− 2a3 ⇒ x = ----= -a. 3a2 3

Mamy stąd

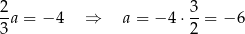
2 3 --a = − 4 ⇒ a = − 4 ⋅--= − 6 3 2

i szukana styczna ma równanie

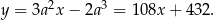
2 3 y = 3a x− 2a = 10 8x+ 432.

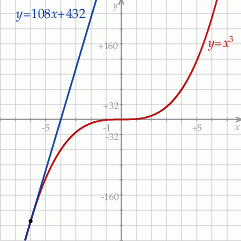
Na koniec wykres dla ciekawskich.

PIC

 
Odpowiedź: y = 1 08x + 432

Wersja PDF