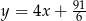Zadanie nr 7842946
Znajdź równanie stycznej do wykresu funkcji 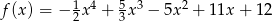 , która jest równoległa do prostej o równaniu
, która jest równoległa do prostej o równaniu 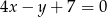 .
.
Rozwiązanie
Musimy sprawdzić w jakim punkcie styczna do wykresu 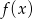 ma współczynnik kierunkowy równy 4. To pytanie to dokładnie pytanie, w jakim punkcie pochodna przyjmuje wartość 4. Liczymy
ma współczynnik kierunkowy równy 4. To pytanie to dokładnie pytanie, w jakim punkcie pochodna przyjmuje wartość 4. Liczymy
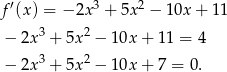
Szukamy teraz pierwiastków wymiernych otrzymanego równania. Łatwo sprawdzić, że jednym z nich jest 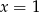 . Dzielimy teraz lewą stronę przez
. Dzielimy teraz lewą stronę przez 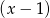 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
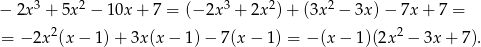
Ponieważ trójmian kwadratowy w drugim nawiasie nie ma pierwiastków (bo ma ujemną 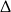 -ę), więc jedynym rozwiązaniem równania
-ę), więc jedynym rozwiązaniem równania 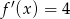 jest
jest 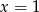 . Mamy ponadto
. Mamy ponadto
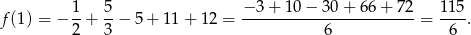
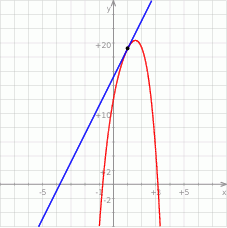
Szukana styczna ma więc równanie
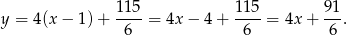
Odpowiedź: