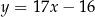/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Styczne do wykresu

Zadanie nr 8624475

Dodaj do ulubionych
Dodaj do rozwiązanych

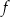Funkcja f jest określona wzorem 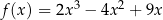3 2 f(x ) = 2x − 4x + 9x dla każdego 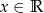x ∈ R . Punkt 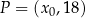P = (x0,18) należy do wykresu funkcji 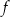f . Oblicz 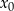x0 oraz wyznacz równanie stycznej do wykresu funkcji 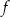f w punkcie P .

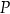Rozwiązanie

Wyznaczmy najpierw 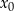x0 . Rozwiązujemy równanie

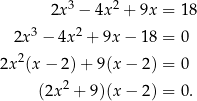
3 2 2x − 4x + 9x = 18 2x 3 − 4x 2 + 9x− 18 = 0 2x 2(x− 2)+ 9(x − 2) = 0 2 (2x + 9)(x − 2) = 0.

Jedynym rozwiązaniem tego równania jest 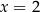x = 2 , czyli 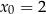x 0 = 2 . Liczymy teraz pochodną funkcji f .

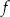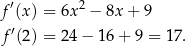
f′(x) = 6x 2 − 8x+ 9 ′ f (2) = 2 4− 16+ 9 = 17.

Korzystamy teraz ze wzoru

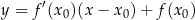
y = f′(x0)(x − x0) + f(x0)

na równanie stycznej do wykresu 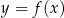y = f (x) . W naszej sytuacji mamy

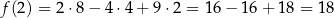
f(2) = 2⋅8 − 4 ⋅4 + 9 ⋅2 = 16 − 16 + 18 = 18

i równanie stycznej ma postać:

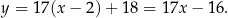
y = 17(x − 2) + 18 = 1 7x− 16.

 
Odpowiedź: 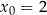x0 = 2 , y = 1 7x− 16

Wersja PDF