/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Styczne do wykresu

Zadanie nr 9490542

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz miarę kąta ostrego pod jakim przecinają się styczne do wykresu funkcji

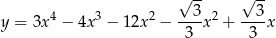
√ -- √ -- y = 3x4 − 4x3 − 12x2 − --3-x2 + --3x 3 3

poprowadzone w punktach o pierwszych współrzędnych równych 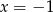x = − 1 i x = 2 .

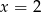Rozwiązanie

Liczymy pochodną danej funkcji.

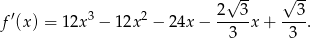
√ -- √ -- f′(x) = 12x 3 − 1 2x2 − 24x − 2-3-x + --3-. 3 3

Obliczamy współczynniki kierunkowe stycznych do wykresu 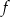f w punktach 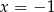x = − 1 i x = 2 .

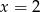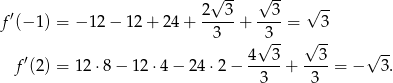
√ -- √ -- ′ 2--3- --3- √ -- f (− 1) = − 12 − 12 + 24 + 3 + 3 = 3 4√ 3- √ 3- √ -- f′(2) = 12 ⋅8 − 12 ⋅4 − 24 ⋅2− -----+ ----= − 3. 3 3

Ponieważ współczynnik kierunkowy prostej jest równy tangensowi kąta jaki ta prosta tworzy z osią 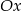Ox , pierwsza styczna przecina oś 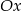Ox pod kątem 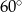60∘ , a druga pod kątem 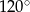1 20∘ . Styczne te przecinają się więc pod kątem 60∘ .

PIC

 
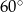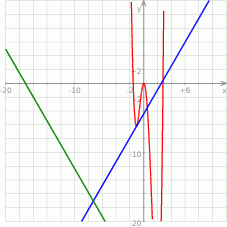
Odpowiedź: 60∘

Wersja PDF