Zadanie nr 2226850
W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu 2. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 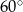 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Zaczynamy od rysunku.
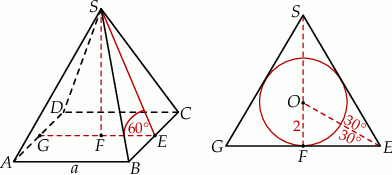
Podana informacja o promieniu kuli wpisanej w ostrosłup oznacza w szczególności, że promień okręgu wpisanego w trójkąt 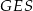 jest równy 2. To zaś pozwala łatwo obliczyć długość krawędzi podstawy.
jest równy 2. To zaś pozwala łatwo obliczyć długość krawędzi podstawy.
Sposób I
Trójkąt 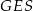 jest równoboczny, więc jeżeli oznaczamy przez
jest równoboczny, więc jeżeli oznaczamy przez  długość jego boku, to
długość jego boku, to
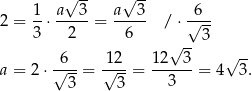
Wysokość ostrosłupa, czyli wysokość trójkąta 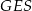 jest 3 razy dłuższa od promienia okręgu wpisanego w ten trójkąt, czyli
jest 3 razy dłuższa od promienia okręgu wpisanego w ten trójkąt, czyli
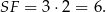
Możemy teraz obliczyć objętość ostrosłupa.
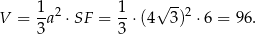
Sposób II
Patrzymy na trójkąt 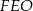 .
.
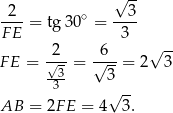
Z trójkąta 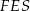 obliczamy długość wysokości
obliczamy długość wysokości 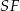 ostrosłupa.
ostrosłupa.
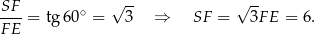
Możemy teraz obliczyć objętość ostrosłupa.
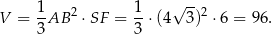
Odpowiedź: 96

