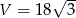/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Objętość

Zadanie nr 2541256

Dodaj do ulubionych
Dodaj do rozwiązanych

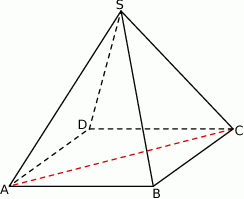
W ostrosłupie prawidłowym czworokątnym 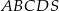ABCDS (zobacz rysunek) przekątna 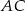AC podstawy ma długość 6. Kąt 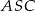ASC między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 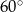60∘ . Oblicz objętość tego ostrosłupa.

PIC

Rozwiązanie

Dorysujmy wysokość ostrosłupa.

PIC

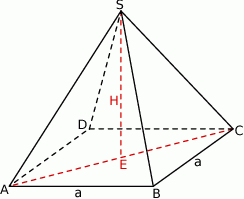
Zauważmy, że trójkąt 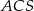ACS jest trójkątem równoramiennym z kątem między ramionami równym 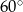60 ∘ , więc jest trójkąt równoboczny. W takim razie, ze wzoru na wysokość w trójkącie równobocznym, możemy obliczyć wysokość ostrosłupa.

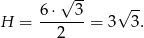
-- 6⋅√ 3 √ -- H = ------= 3 3. 2

W podstawie ostrosłupa jest kwadrat o boku a i przekątnej długości 6, więc

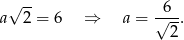
√ -- 6 a 2 = 6 ⇒ a = √--. 2

Liczymy objętość ostrosłupa.

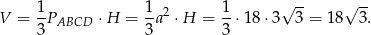
√ -- √ -- V = 1PABCD ⋅H = 1a2 ⋅ H = 1-⋅18 ⋅3 3 = 1 8 3. 3 3 3

 
Odpowiedź: √ -- V = 18 3

Wersja PDF