Zadanie nr 4013588
Pole podstawy ostrosłupa prawidłowego czworokątnego jest równe 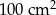 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 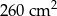 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Zacznijmy od rysunku.
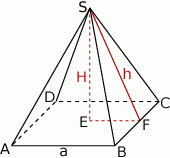
Wiemy, że kwadrat w podstawie ma pole 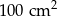 , więc jego bok ma długość 10 cm. W takim razie z podanego pola powierzchni bocznej mamy równanie
, więc jego bok ma długość 10 cm. W takim razie z podanego pola powierzchni bocznej mamy równanie
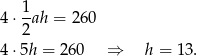
Z trójkąta prostokątnego 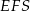 mamy
mamy
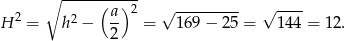
Objętość ostrosłupa jest więc równa
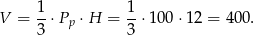
Odpowiedź: