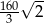/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Objętość

Zadanie nr 5828933

Dany jest ostrosłup prawidłowy czworokątny o podstawie 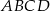ABCD i wierzchołku 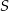S . Pole trójkąta 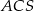ACS jest równe 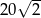√ -- 20 2 , krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 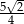5√-2 4 . Oblicz objętość ostrosłupa.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku

PIC

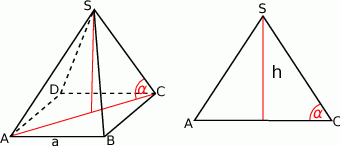
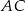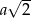Odcinek AC jest przekątną kwadratu o boku długości a , więc jej długość wynosi √ -- a 2 . Zapisujemy układ równań wynikający z założeń

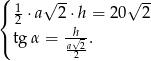
( √ -- √ -- { 1⋅ a 2⋅h = 20 2 2 -h- ( tg α = a√2. 2

Stąd

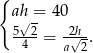
{ ah√ = 40 542-= -2√h-. a 2

Wyznaczamy z drugiego równania 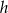h

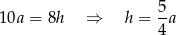
5 10a = 8h ⇒ h = 4a

i podstawiamy do pierwszego równania.

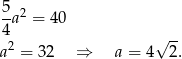
5-2 4a = 4 0 2 √ -- a = 32 ⇒ a = 4 2.

Zatem

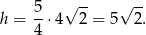
√ -- √ -- h = 5⋅ 4 2 = 5 2. 4

Teraz już łatwo policzyć objętość

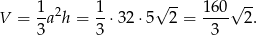
1 1 √ -- 160 √ -- V = -a2h = -⋅ 32⋅5 2 = ---- 2. 3 3 3

 
Odpowiedź: √ -- 1630 2

Wersja PDF